Question

Найдите площадь фигуры, ограниченной кривой

Answer 1

***

астроида — это плоская кривая, описываемая точкой окружности радиуса, катящейся по внутренней стороне окружности радиуса;

с модулем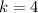  ${\displaystyle k=4}$

(R=10)

${\displaystyle x^{2/3}+y^{2/3}=R^{2/3}}$  

$x^{2/3} +y^{2/3} =10^{2/3}$

запишем параметрическое уравнение:

$\left \{ { x=R\cos ^{3}t}} \atop {y=R\sin ^{3}t}} \right. \left \{ {{x =10cos^3t} \atop {y=10sin^3t}} \right.$

будем находить площадь одной четвёртой части фигуры (см. рис.) и полученное умножим на 4

$0\leq x\leq 10pi/2 \leq t \leq 0$

=>

$x_{1} =0$      <=>     $10cos^3t=0$     <=>   $cost=0$   $t_{1} =\pi /2$

$x_{2} = 10$    <=>      $10cos^3 t = 10$   <=>   $cost=1$  $t_{2} = 0$

$S/4 = \int\limits^{t_{2} }_{t_{1}} {y(t) ^{.}x'(t) } \, dt =\int\limits^0_{\pi /2} {10sin^3t^. (-30cos^2 t ^.sint)} \, dt = -\int\limits^{\pi /2}_0 {-300sin^4t^.cos^2t} \, dt =$

$300\int\limits^{\pi /2}_0 {sin^2t ^. sin^2 t^.cos^2t} \,^. dt = 300\int\limits^{\pi /2}_0 {\frac{1-cos2t}{2}^.(1/2sin2t)^2 } \, dt =$

$\frac{300}{8} \int\limits^{\pi /2}_0 {(sin^22t-sin^22t^.cos2t}) \, dt = \frac{300}{8} ^.(\int\limits^{\pi /2}_0 {\frac{1-cos4t}{2} \, dt - \frac{1}{2} \int\limits^{\pi /2}_0 {sin^22t^.} d(sin2t))=$

$\frac{300}{16} ^. (t - \frac{sin4t}{4} ) |_{0} ^{\pi /2} - \frac{300}{16} ^. \frac{sin^32t}{3} |_{0} ^{\pi /2=$

$\frac{300}{16} ^{.} \frac{\pi}{2} = \frac{300\pi }{32}$

$S = 4 ^. (\frac{300}{32}) =\frac{75\pi }{2}$

ответ: 75п/2