Числа 7. Три числа утворюють геометричну прогресію. Якщо друге число збільшити на 2, ТО утворюватимуть арифметичну прогресію, а якщо після цього збільшити останнє число на 9, то знову утвориться геометрична прогресія. Знайдіть три вихідні числа.
Находим время, в течение которого поезда будут следовать друг мимо друга: t=(s₁+s₂)/(v₁+v₂)=(0,35км+0,42км)/(60км/ч+50км/ч)=0,007ч Находим искомое расстояние следующим образом: узнаем какое расстояние проехал поезд за время встречи 0,007ч и отнимем от этого расстояния длину поезда: Для первого поезда: l=v₁t-s₁=60км/ч·0,007ч-0,35км=0,07км=70м Для второго поезда: l=v₂t-s₂=50км/ч·0,007ч-0,42км=-0,07км=-70м Результаты получились противоположными, так как поезда едут в противоположных направлениях. В ответ идет модуль любого значения. ответ: 70 метров
В подобных задачах обычно используется теорема Пифагора и синусы, косинусы, тангенсы острых углов.
Теорема Пифагора может пригодится, если известно две стороны из трёх. a² = b² + c² a - гипотенуза; b, c - катеты.
Теперь остановимся на острых углах.
1) Один острый угол равен 45°. В таких задачах прямоугольный треугольник ещё и равнобедренный ⇒ равны катеты.
2) Один из острых углов равен 30° (60°). Есть одна теорема: напротив угла в 30° лежит катет в два раза меньше гипотенузы. Для большей наглядности возьмём треугольник ABC (∠C - прямой). Пусть ∠А = 30°, тогда AB (гипотенуза) = 2*BC (катет, напротив 30°)
3) Обычно острые углы в прямоугольном треугольнике либо равны 30°, 45°, 60°, либо даны синусы, косинусы, тангенсы этих углов ( например, tgA = 2) В таких случаях надо выражать тангенс, синус или косинус через стороны.
Например в треугольнике ABC (∠C - прямой) BC = 14, а tgA = 2. Нужно найти AC. Тангенс - отношение противолежащего катета к прилежащему, то есть tgA = BC : AC, подставив значения, находим AC = 7.
Приведу второй пример. Треугольник ABC (∠C - прямой), ∠A = 30°, AB = 8. Найти BC. Такую задачу можно решить по теореме, указанной выше под цифрой 2, или выразив сторону BC через синус. Синус - отношение противолежащего катета к гипотенузе, то есть sinA = BC : AB. sinA = sin30° = 1/2. Подставив значения, находим BC = 4.
Объяснение:
Пусть три исходных числа, образующих геометрическую прогрессию —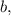
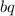 и
и 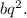
Тогда тройка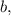
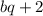 и
и 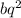 будет составлять арифметическую прогрессию. Пользуясь характеристическим свойством арифметической прогрессии
будет составлять арифметическую прогрессию. Пользуясь характеристическим свойством арифметической прогрессии
запишем
Тройка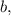
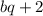 и
и 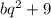 снова будет образовывать геометрическую прогрессию. Пользуясь характеристическим свойством геометрической прогрессии
снова будет образовывать геометрическую прогрессию. Пользуясь характеристическим свойством геометрической прогрессии
запишем
Получили систему двух уравнений с двумя неизвестными:
Преобразуем первое уравнение:
Преобразуем второе уравнение:
Приравняем найденные выражения для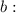
По теореме Виета
откуда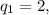
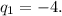
Тогда
Получаем две тройки подходящих чисел: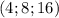 и
и ![\[\left( {\displaystyle\frac{4}{{25}};\,\, - \displaystyle\frac{{16}}{{25}};\,\,\displaystyle\frac{{64}}{{25}}} \right).\]](/tpl/images/4978/6404/cbc9d.png)