(х+1)(х+2)(х+4)(х+5) и (у-3)(у-4)(у-6)
Объяснение:
для облегчения можно разделить число на сумму , а затем вынести отдельно за скобки.
так же во втором при вынесении числа за скобки , возможно , покажется неправильным появление отрицательного числа , но это не так; при произведении двух отрицательных чисел получается положительное.
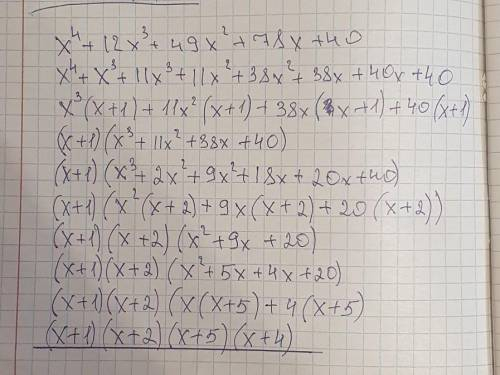
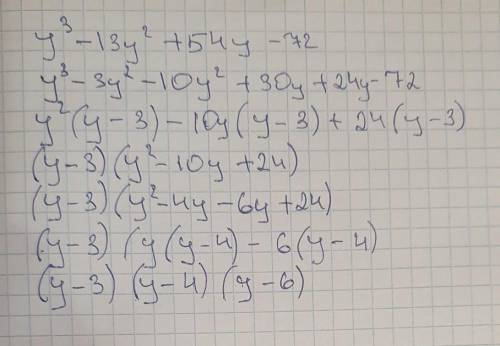
40 ч
Объяснение:
I труба II труба Обе трубы
Работа 1 1 1
Время х-16 х 15
Производительность 1/(х-16) 1/х 1/15
x-16>0, x>16
Составим уравнение:
1/(х-16) + 1/х = 1/15
15х+15(х-16) = х(х-16)
15x+15x-240=x²-16x
x²-46x+240=0
D=(-46)²-4*1*240=1156=34²
x₁=(46+34)/2=40
x₂=(46-34)/2=6 (<16) - не подходит
х = 40 ч - время, за которое будет опустошаться бассейн только второй трубой
Неравенства с модулем
|x^2 - 2x + 2| + |2x + 1| <= 5
Линейные
7x - 6 < x + 12
С квадратом
-3x^2 + 2x + 5 <= 0
Со степенью
2^x + 2^3/2^x < 9
С кубом (неравество третьей степени)
2x^3 + 7x^2 + 7x + 2 < 0
С кубическим корнем
cbrt(5x + 1) - cbrt(5x - 12) >= 1
С натуральным логарифмом
(ln(8x^2 + 24x - 16) + ln(x^4 + 6x^3 + 9x^2))/(x^2 + 3x - 10) >= 0
Иррациональные с квадратным корнем
sqrt(x - 2) + sqrt(x - 5) <= sqrt(x- 3)
Показательные неравенства
8^x + 18^x > 2*27^x
Логарифмические неравенства
log(((7 - x)/(x + 1))^2)/log(x + 8) <= 1 - log((x + 1)/(x - 7))/log(x + 8)
Тригонометрические
tg(x - pi/3) >= -sqrt(3)
Квадратное неравенство
25x^2 - 30x + 9 > 0
С четвёртой степенью
(x - 6)^4*(x - 4)^3*(x + 6)/(x - 7) < 0
С дробью
2x^2 - 15x + 35 - 30/x + 8/x^2 >= 0
Решение с целыми числами
(4x^2 - 3x - 1)/(2x^2 + 3x + 1) > 0
1) Подберём первый корень . Он должен находиться среди делителей свободного члена , числа 40 . При подстановке х= -4 в уравнение получим 0 , значит х= -4 - корень многочлена. Значит можно выделить скобку (х-(-4))=(х+4) .
Опять подбираем корень для многочлена 3 степени среди делителей числа 10 . Это будет х= -5 . И выделяем скобку (х+5) .
3) Аналогично решаем второй пример. Подбираем первый корень, у=4 и выделяем скобку (х-4) .