О данном животном было упомянуто в книге “Индика”. К сожалению, труды врача не дошли до наших дней, но существует большое количество произведений других авторов, которые опирались на суждения Ктесия. Необходимо сказать, что благодаря этому врачу грекам стали известны многие мифические существа. Более ясное описание о животном сложилось только ко 2 веку до нашей эры, его сделал Клавдий Элиан. Но существовали и деятели, которые не верили в мантикору. Так, греческий географ Павсаний не признавал эти писания про мифическое животное и говорил, что это
Источник: https://mifistoria.info/mantikora
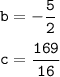
Объяснение:
Даны касательные y₁ = 4·x и y₂ = -9·x к графику функции f(x)=x²+b·x+c.
Пусть прямая y₁ касается к графику функции f(x) в точке x₁, а прямая y₂ касается к графику функции f(x) в точке x₂, то есть:
f(x₁) = y₁(x₁), f'(x₁) = y₁'(x₁) , f(x₂) = y₂(x₂), f'(x₂) = y₂'(x₂) (1).
Так как y₁' = (4·x)' = 4, y₂' = (-9·x) = -9 и f'(x) = (x²+b·x+c)'=2·x+b, то подставляя в уравнения (1) получим 4 уравнения:
x₁²+b·x₁+c = 4·x₁ (2)
2·x₁+b = 4 (3)
x₂²+b·x₂+c = -9·x₂ (4)
2·x₂+b = -9 (5)
Из (3) получим x₁ = (4-b)/2 и подставим в (2):
((4-b)/2)²+b·((4-b)/2)+c = 4·(4-b)/2 или
4-2·b+b²/4+2·b-b²/2+с=8-2·b.
Упростив последнее равенство и получим:
c=4+b²/4-2·b. (6)
Из (5) получим x₂ = (-9-b)/2 и подставим в (4):
((-9-b)/2)²+b·((-9-b)/2)+c = -9·(-9-b)/2 или
81/4+9·b/2+b²/4-9·b/2-b²/2+с=81/2+9·b/2.
Упростив последнее равенство и получим:
c=81/4+b²/4+9·b/2. (7)
Приравниваем выражения (6) и (7):
4+b²/4-2·b = 81/4+b²/4+9·b/2 или
13·b/2 = 4-81/4.
Отсюда
b = (-65/4):(13/2) = -5/2.
Подставим последнее в (6):
c= 4+(-5/2)²/4-2·(-5/2) = 4+25/16+5 = 9+25/16 = 169/16.
1) хз
2)4x²+4x+1 ≤ 0
(2х1)²<0
(2х1)²=0
1
х= - —
2