Правильного ответа среди предложенных нет, но возможно там опечатка и ответ В
Объяснение:
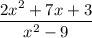
Разберём отдельно числитель и знаменатель
1) 2x²+7x+3
Для нахождения корней этого выражения, приравняем его к нулю
2x²+7x+3 = 0;
D = 7²-4*2*3 = 49-24 = 25 = 5²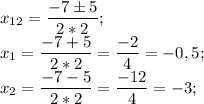
Выражение типа ax²+bx+c можно разложить как a(x-x₁)(x-x₂), из этого следует, что 2x²+7x+3 = 2(х+0,5)(х+3) = (2х+1)(х+3)
2) x²-9
Исходя из формулы разности квадратов a²-b² = (a-b)(a+b) мы можем сделать вывод, что x²-9 = (х-3)(х+3)
- - - - - - - - - - - - - - -
Вернёмся к исходному выражению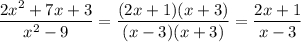
ответ: Щоб розв'язати систему рівнянь, можна скористатися методом підстановки або методом елімінації.
Метод підстановки:
1. З першого рівняння виразимо х:
2x + 3y = 3
2x = 3 - 3y
x = (3 - 3y) / 2
2. Підставимо отримане значення х в друге рівняння:
3y² - 4x = 18
3y² - 4((3 - 3y) / 2) = 18
3y² - 6 + 6y = 18
3y² + 6y - 24 = 0
3. Розв'яжемо квадратне рівняння:
(3y - 6)(y + 4) = 0
Звідси отримуємо два розв'язки:
3y - 6 = 0 або y + 4 = 0
y = 2 або y = -4
4. Підставимо знайдені значення y в перше рівняння для знаходження відповідних значень x:
При y = 2:
2x + 3(2) = 3
2x + 6 = 3
2x = -3
x = -3/2
При y = -4:
2x + 3(-4) = 3
2x - 12 = 3
2x = 15
x = 15/2
Отже, розв'язками системи рівнянь є:
x = -3/2, y = 2
x = 15/2, y = -4
Объяснение:
1) Множество точек, удовлетворяющих неравенству ,
,
Множество точек, удовлетворяющих неравенству
лежат внутри окружности с центром в точке ( 1 : 0) , радиуса R=2 .
2) Множество решений системы неравенств изображено на рисунке.
Область заштрихована . Это полоса между прямыми х= -2 и х=2 , расположенная выше прямой у=3 . Сами прямые в область не входят, так как неравенства имеют строгие знаки .
3) Фигура, изображённая на рисунке, может быть задана с системы неравенств .
.
Неравенство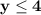 описывает множество точек, лежащих ниже прямой у=4 .
описывает множество точек, лежащих ниже прямой у=4 .
Неравенство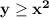 описывает множество точек, расположенных внутри параболы
описывает множество точек, расположенных внутри параболы 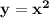 . Это можно определить, если рассматривать точку , которая находится внутри параболы , например, точка (1;2) , и точку с той же абсциссой х=1 , лежащую на параболе, имеющую ординату у=1²=1 . Сравним ординаты этих точек: 2>1 . Значит ординаты точек, находящихся внутри параболы, больше , чем ординаты точек, лежащих на параболе . Отсюда и получаем у≥х² .
. Это можно определить, если рассматривать точку , которая находится внутри параболы , например, точка (1;2) , и точку с той же абсциссой х=1 , лежащую на параболе, имеющую ординату у=1²=1 . Сравним ординаты этих точек: 2>1 . Значит ординаты точек, находящихся внутри параболы, больше , чем ординаты точек, лежащих на параболе . Отсюда и получаем у≥х² .