По условию получаем систему уравнений (если х×у=-75), то:
1-е число-х
2-е число-у
{х+у=20
{х×у=-75
х=(20-у)
(20-у)×у=-75
-у²+20у=-75
у²-20у-75=0
D=(-(-20))²-4×1×(-75)=400+300=700
у1=(-(-20)-√700)/2×1=(20-√700)/2=(20-26,46)/2=-6,46/2=-3,23
у2=(-(-20)+√700)/2×1=(20+26,46)/2=46,46/2=23,23
х1=20-y1
x1=20-(-3,23)
x1=23,23
x2=20-y2
x2=20-23,23
x2=-3,23
проверка: х1×у1=-75
23,23×(-3,23)=-75
-75,0329≈-75
ответ: (23,23;-3,23) и (-3,23;23,23)
если (х×у=75), то
{х+у=20
{х×у=75
х=(20-у)
(20-у)×у=75
20у-у²=75
у²-20у+75=0
D=(-(-20))²-4×1×75=400-300=100
y1=(-(-20)-√100)/2×1=(20-10)/2=10/2=5
y2=(-(-20)+√100)/2×1=(20+10)/2=15
x1=20-y1
x1=20-5
x1=15
x2=20-y2
x2=20-15
x2=5
ответ: (15;5) и (5;15).
7/12
Объяснение:
Заштрихованная фигура состоит из двух криволинейных трапеций. Одна, находящаяся над осью абсцисс, ограничена графиком y = x², двумя вертикальными прямыми x = -1 и x = 0, а также самой осью Ox. Вторая, находящаяся под осью абсцисс (из-за этого ее площадь возьмем со знаком минус), ограничена графиком y = x³, теми же вертикальными прямыми и той же осью Ox.
Тогда площадь S рассматриваемой фигуры будет равна сумме двух определенных интегралов (один — от x², другой — от x³ со знаком минус), оба вычисленных на отрезке [-1; 0]:
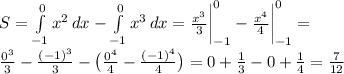

х = 4
Объяснение: