Число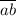 
по определению десятичной записи представимо в виде 
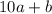. Точно также, например, 
, 
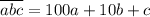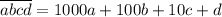и т. д.
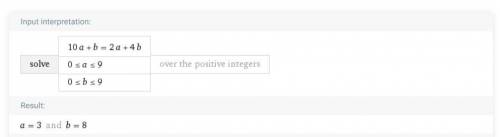
В задаче 24 получаем уравнение:
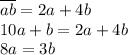
Поскольку 
и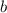 
цифры двузначного числа, то 
.
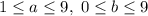Чтобы выполнилось последнее равенство, надо найти общее кратное чисел 8 и 3. В данном случае найдём НОК(8,3), которое равно 24. Тогда а=3, b=8, а сумма a+b=11. Можно легко перебрать из неравенства, что других решений нет (если взять какое-нибудь большее кратное, то a или b станет больше девяти).
***
Вторая задача решается точно так же. Дам решение уже без объяснений.
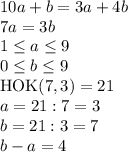
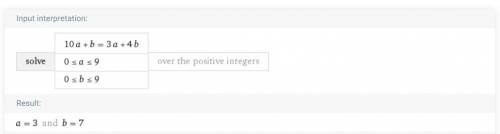
В решении.
Объяснение:
Решите задачу с составления уравнения. Разность двух чисел равна 25, а разность их квадратов 875. Найдите эти числа.
х - первое число.
у - второе число.
По условию задачи система уравнений:
х - у = 25
х² - у² = 875
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 25 + у
(25 + у)² - у² = 875
625 + 50у + у² - у² = 875
50у = 875 - 625
50у = 250
у = 250/50
у = 5 - второе число.
х = 25 + у
х = 25 + 5
х = 30 - первое число.
Проверка:
30 - 5 = 25, верно.
30² - 5² = 900 - 25 = 875, верно.
(х-4)(х+5)-(х-7)(х+7)=-7
x(x + 5) - 4(x + 5) - (x - 7)(x + 7) = - 7
x ^ 2 + 5x - 4(x + 5) - (x - 7)(x + 7) = - 7
x ^ 2 + 1x - 20 - (x - 7)(x + 7) = - 7
x ^ 2 + x - 20 - (x(x + 7) - 7(x + 7)) = - 7
x ^ 2 + x - 20 - (x ^ 2 + 7x - 7(x + 7)) = - 7
x ^ 2 + x - 20 - (x ^ 2 + 7x - 7x - 49) = - 7
x ^ 2 + x - 20 - (x ^ 2 - 49) = - 7
x ^ 2 + x - 20 - x ^ 2 + 49 = - 7
x ^ 2 + x + 29 - x ^ 2 = - 7
x + 29 = - 7
x + 29 - 29 = - 7 - 29
x = - 36
Відповідь: - 36