Отметь как лучший,буду рад!
1)Множество целых чисел Z включает в себя число 0, множество натуральных чисел и отрицательные числа .
2) Множество рациональных чисел Q включает в себя множество целых чисел Z и все дробные числа.
3) Вместо фразы m – целое число можно писать Z .
4) Вместо фразы r– рациональное число можно писать Q.
5) N – множество натуральных чисел множества Z , Z – множество целых чисел множества Q.
6) Повторяющая группа цифр после запятой в записи десятичной дроби называется периодом, а сама дробь называется периодической.
7) Множество Q рациональных чисел - это множество чисел вида m/n ,
где - m целое число, n – натуральное число , или как множество обыкновенных дробей.
Объяснение:
y = x² - 2x - 8 a = 1; b = -2; c = -8
Квадратичная функция, график - парабола, ветви направлены вверх (a=1>0). Координаты вершины :
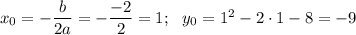
Точки для построения
x | -3 -2 -1 0 2 3 4 5
y | 7 0 -5 -8 -8 -5 0 7
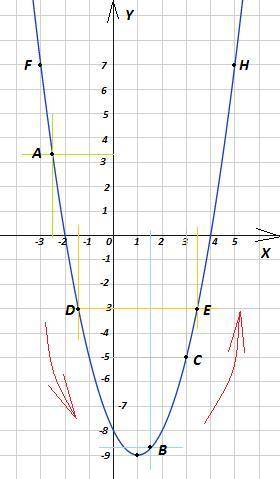
График в приложении.
a) x = -2,5; y = 3,25 Точка А
x = 1,5; y = -8,75 Точка В
x = 3; y = -5 Точка С
б) y = -3; x₁ ≈ -1,45; x₂ ≈ 3,45 Точки D и Е
y = 7; x₁ = -3; x₂ = 5 Точки F и H
в) y↑ при x ∈ [-1; +∞)
y↓ при x ∈ (-∞; 1]
Чтобы найти наибольшую скорость движения материальной точки, необходимо взять производную от функции s(t) по времени t и найти значения времени, при которых производная равна нулю. Затем, среди найденных значений выбрать наибольшее.
Дано:
s(t) = -t³ + 18t² - 60t
Чтобы найти скорость, возьмем производную s(t) по t:
v(t) = ds(t)/dt
v(t) = d/dt(-t³ + 18t² - 60t)
v(t) = -3t² + 36t - 60
Теперь найдем значения времени t, при которых производная равна нулю:
-3t² + 36t - 60 = 0
Для решения этого квадратного уравнения можно использовать квадратное уравнение или графический метод. Но в данном случае, можно заметить, что уравнение можно упростить, разделив все его члены на -3:
t² - 12t + 20 = 0
Это квадратное уравнение можно разложить на множители:
(t - 10)(t - 2) = 0
Отсюда получаем два значения времени: t = 10 и t = 2.
Теперь нужно выбрать наибольшее значение времени, чтобы найти наибольшую скорость. В данном случае, это t = 10.
Таким образом, наибольшая скорость движения материальной точки достигается при t = 10. Чтобы найти эту скорость, подставим t = 10 в выражение для скорости:
v(10) = -3(10)² + 36(10) - 60
v(10) = -3(100) + 360 - 60
v(10) = -300 + 360 - 60
v(10) = 0
Наибольшая скорость движения материальной точки равна 0.