В решении.
Объяснение:
Построить график функции у=(х-2)²-2.
Такой вид уравнения полезен только для определения координат вершины параболы: (х-2)² - смещение вершины вправо по оси Ох на 2 единицы от начала координат, свободный член с= -2 показывает смещение вершины вниз по оси Оу на 2 единицы от начала координат, координаты вершины параболы (2; -2).
Чтобы заполнить таблицу, нужно развернуть уравнение, тогда будет видна и точка пересечения графиком оси Оу:
у=(х-2)²-2
у=х²-4х+4-2
у=х²-4х+2
Парабола пересекает ось Оу в точке у=2.
Координаты точки пересечения (0; 2)
Придаём значения х, вычисляем у, заполняем таблицу.
Таблица:
х -2 -1 0 1 2 3 4 5 6
у 14 7 2 -1 -2 -1 2 7 14
x∈[-1, 1)∪(3, 5]
Объяснение:
Решить систему неравенств:
х²-4х+3<=8
(x-3)(x-1)>0
Первое неравенство. Решить как квадратное уравнение:
х²-4х+3=8
х²-4х+3-8=0
х²-4х-5=0, ищем корни:
х₁,₂=(4±√16+20)/2
х₁,₂=(4±√36)/2
х₁,₂=(4±6)/2
х₁= -2/2
х₁= -1
х₂=10/2
х₂=5
Начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -1 и х=5. По графику ясно видно, что у<=0 при х от -1 до 5, то есть, решения неравенства находятся в интервале
х∈ [-1, 5], это решение первого неравенства.
Неравенство нестрогое, значения х= -1 и х=5 входят в число решений неравенства, скобки квадратные.
Второе неравенство. Также решим как квадратное уравнение, удобнее определять интервалы решений неравенства:
(x-3)(x-1)>0
х²-х-3х+3>0
х²-4х+3>0, ищем корни:
х₁,₂=(4±√16-12)/2
х₁,₂=(4±√4)/2
х₁,₂=(4±2)/2
х₁=2/2
х₁=1
х₂=6/2
х₂=3
Снова чертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 1 и х=3. По графику ясно видно, что у>0 при х влево и вправо от точек пересечения параболой оси Ох, то есть,
х∈(-∞, 1)∪(3, +∞). Это решение второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно найти пересечение решений неравенств, то есть, такое решение, которое подходит и первому, и второму неравенствам.
На числовой оси отмечаем точки -1, 1, 3, 5. Наносим штриховку в соответствии с двумя решениями.
Находим пересечение: x∈[-1, 1)∪(3, 5], то есть решения системы неравенств находятся в интервале при х от -1 до 1, и от 3 до 5.
Значения х= -1 и х=5 входят в число решений системы, скобка квадратная, значения х=1 и х=3 не входят в число решений, скобка круглая.
Відповідь:
1) 10
2) Доведення нижче
3) Доведення нижче
4) Доведення нижче
Пояснення:
1)
7921-121=7800 (млинців) 1936-1156=780 (гостей)
2)
Тоді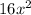
+40x+25-9= 
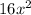+40x+16
ТЕПЕР УВАЖНО, число ділиться на 4 якщо два останніх числа утворюють число, що ділиться на 4. Я підставляв замість x числа 111, 3, 1, 103, 78 - утворене число завжди ділилося на 4. Це, як я зрозумів,
відбувається із-за чисел в нашому рівнянні: 16 та 40 (що і є кратними 4), а при множенні ми тільки збільшуємо їх кількість (як приклад, якщо підставити замість x=2, то рівняння можна записати буде так: 16*4+40*2+16 або 16+16+16+16+40+40+16, а тут в будь-якому випадку число буде ділитися на 4, бо всі числа в рівняння мають один і той самий дільник).
3) Взагалі, я не знайшов формули, де степені можна легко додати чи відняти, тільки за до розрахунків (якщо я помиляюсь, то напишіть в коментарях як можна вирішити цю задачу).
Так от,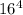
=65536
65536-16384+2048=51200 (ЦЕ ЧИСЛО ДІЛИТЬСЯ на 25, утворюючи 2048)
*Міцний вчитель, спробуй підготувати 51200 карток)
4) Теж саме, що й в минулій задачі.
Тоді 244 140 625 - 2*9 765 625 =244 140 625 - 19 531 250=224 609 375 (це число ділиться на 23)
*Усім учням точно хватить стільців