см, тогда второй катет - 
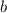см. Площадь прямоугольного треугольника равна 
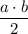, что составляет 210 см² или перепишем сразу 
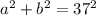
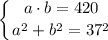
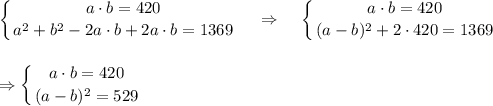
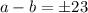. Тогда имеем несколько случаев.
, то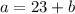 
и подставим в первое уравнение.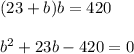
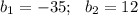см и корень 
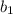не удовлетворяет заданному условию
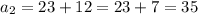см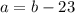
,то подставив в первое уравнение, получим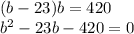
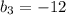
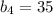см и корень 
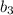не удовлетворяет условию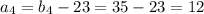
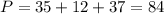см
(-∞; - 1] U [3; + ∞)
Объяснение:
(1/2)^(х² - 2х) ≤ 1/8
(1/2)^(х² - 2х) ≤ (1/2)^3
Так как 0 < 1/2 < 1, то функция у = (1/2)^t убывающая, тогда
х² - 2х ≥ 3
х² - 2х - 3 ≥ 0
D = 4+12 = 16
x1 = (2+4)/2 = 3;
x2 = (2-4)/2 = - 1;
(x - 3)(x + 1) ≥ 0
y = (x - 3)(x + 1)
Нули функции:
х = 3 и х = - 1.
__+__ [-1]__-__[3]___+___ x
у ≥ 0 при x є (-∞; - 1] U [3; + ∞)