на 20%
Объяснение:
19 секунд — 100%
15,2 секунды — х %
19/15,2 = 100/х
19 * х = 15,2 * 100
19х = 1520
х = 1520 : 19
х = 80
100% - 80% = 20% - время разгона больше 1 автомобиля
:
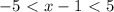
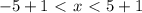
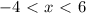
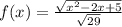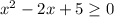
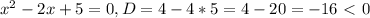
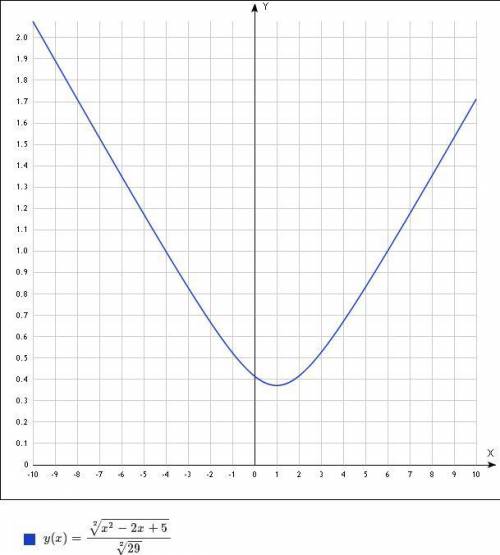
- парабола ветвями вверх, то неравенство выполняется для любых х.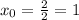
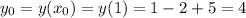
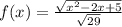принимает в вершине параболы х=1: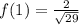
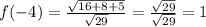
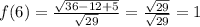
Відповідь: 25%
Пояснення: Щоб знайти відсоток, на який час розгону першого автомобіля більший, ніж другого, необхідно порівняти різницю часів розгону з часом розгону другого автомобіля, а потім виразити результат у відсотках.
Різниця часів розгону:
19 с - 15,2 с = 3,8 с
Відсоток, на який час розгону першого автомобіля більший за другий, можна обчислити за формулою:
(різниця часів / час розгону другого автомобіля) * 100
(3,8 с / 15,2 с) * 100 ≈ 25
Отже, час розгону першого автомобіля більший на приблизно 25 відсотків порівняно з другим автомобілем.