2(x - 5) - 4(x+3)=x-43
2x-10-4x-12=x-43
2x-22-4x=x-43
-2x-22=x-43
-2x-22+22=x-43+22
-2x=x-21
-2x-x=x-21-x
-3x=-21
x=-21:(-3)
x=7
, 
, 
, 
, 
, 
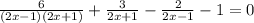
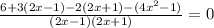
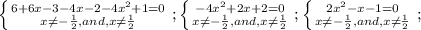
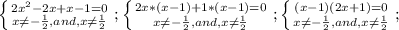
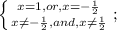
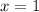
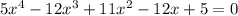
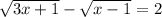
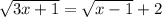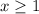
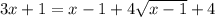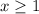
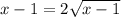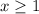
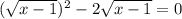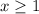
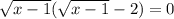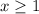
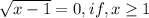
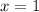
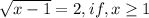
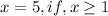
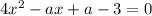
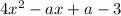- парабола ветками вверх, нам нужен случай, когда вершина параболы лежит на оси ОХ, т.е. когда парабола пересекает эту ось в одной точке.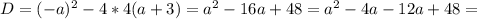
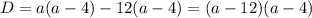
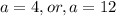
Давайте розв'яжемо рівняння крок за кроком:
2(x - 5) - 4(x + 3) = x - 43
Розкриваємо дужки:
2x - 10 - 4x - 12 = x - 43
Складаємо подібні доданки:
-2x - 22 = x - 43
Переносимо всі змінні на один бік, а всі константи на інший:
-2x - x = -43 + 22
-3x = -21
Ділимо обидві сторони на -3:
x = 7
Тож розв'язком рівняння є x = 7.