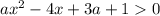
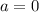квадратное неравенство вырождается в линейное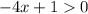
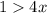
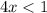
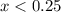
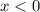
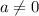
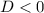) - отлично, график параболы выше оси Ох - неравенство выполняется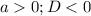
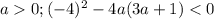
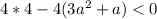
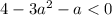
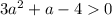
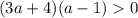
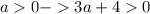авмтоматически
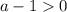или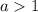 
- 
; 
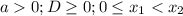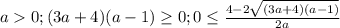
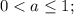- с первых двух неравенств (аналогично по рассуждениям относительно первого случая)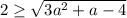
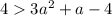
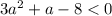- что очевидно верно при условиях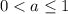 
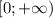
Отдельный случай
а значит выполняется для всех
Пусть теперь
квадратное неравенство, чтоб оно выполнялось
нужно чтоб ветви параболы были направлены верх
(очевидно если ветви будут вниз то найдется гдето точка ближе к минус бесконечности так точно для которой значение функции задающей л.ч неравенства будет отрицательно, так как в случае ветвей вниз, только ограниченная часть параболы находится выше оси абсцис)
итак имеем первое необходимое условие
дальше два случая
первый случай - если корней нет (
УчитЫвая второе условие
и необходимо вЫполнение неравенства
теперь рассмотрим второй случай
когда есть корни -точки пересечения с осью абсцисс - необходимо чтоб левый(меньшее число) (или единственный --одинаковый) корень лежал правее 0 (или равнялся 0)[/tex]
итого
обьединяя все
получаем что данное неравенство верно при
а є