Объяснение:
СМЕНА ЗНАКА В НЕРАВЕНСТВАХ
И логарифмическая, и показательная функция могут быть либо монотонно убывающей (при основании < 1 ), либо монотонно возрастающей ( при основании больше 1 ). Если функция является монотонно возрастающей, тогда ее значение будет тем больше, чем больше аргумент. Поэтому, если основание логарифма или основание показательной функции больше 1, то при снятии логарифма или экспоненты знак неравенства сохраняется. Если функция монотонно убывает, то ее значение тем меньше, чем больше аргумент. Поэтому, при основании меньше 1 знак неравенства изменяется на противоположный.
Это очень важное свойство, о котором, тем не менее, очень часто забывают.
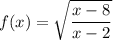
Подкоренное выражение должно быть неотрицательным, а знаменатель не равен нулю. При записи первого условия, второе учитывается. Тогда имеем:
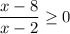
Решим методом интервалов:
Отмечаем на координатной прямой точки, в которых выражения из знаменателя и числителя обращаются в ноль. И выкалываем 2 т.к. на ноль делить нельзя. Мы получили 3 интервала. Перед дробью знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая их границы.
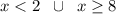
ответ: x∈(-∞;2)∪[8;+∞).

Відповідь: рівняння прямої y = - 2x .
Пояснення:
Пряма проходить через початок координат , тому ця залежність
є прямою пропорційністю виду у = kx ;
L( 2 ;- 4 ) : - 4 = k * 2 ; > k = - 4 : 2 ; > k = - 2 ; y = - 2x .