(6x²-13x+1)/(2x-5) разделим:
3x+1+(6/(2х-5)). - тогда в знаменателе должно быть число кратное 6-ти: -6, -3, -2, -1, 1, 2, 3, 6. Тогда х₁=1, х₂=2, х₃=3, х₄=4.
1) c² + b³ - cb + c - cb² - b² = (c² - cb + c) + (b³ - cb² - b²) =
= c(c - b + 1) + b²(b - c - 1) = c(c - b + 1) - b²( c - b + 1) = (c - b + 1)(c - b²)
2) (x + y - 7)² + (x - 2y + 2)² = 0
Это равенство верно только в случае, когда :
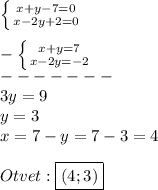
3) Пусть надо взять х кг 25% - го и y кг 50% - го сплавов меди . Надо получить 20 кг 40% - го сплава.
x y 20 = x + y
25% 50% 40%
0,25x + 0,5y = 0,4(x + y)
Если x + y = 20 , то y = 20 - x
0,25x + 0,5 * (20 - x) = 0,4 * 20
0,25x + 10 - 0,5x = 8
- 0,25x = - 2
x = 8 кг - 25% - го
y = 20 - 8 = 12 кг - 50% - го
ответ : надо взять 8 кг 25% - го и 12 кг 50% - го сплавов
делим столбиком это выражение (6x²-13x+1)/(2x-5)=3х+1+ (6/(2х-5))
далее чтобы дробь была целым числом, в знаменателе нужна -6 или -3 или -2 или -1 или 1 или 2 или 3 или 6, значит х=1, 2, 3 и 4