Объяснение:
Можно, конечно, сказать, что точки пересечения (общие точки графиков) функций определяются системой уравнений
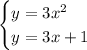
и решать ее.
Однако, гораздо проще заметить, что точка пересечения - это точка (х; у), такая, что значения х, у одинаковы жля обоих уравнений.
А значит, можно просто приравнять правые части
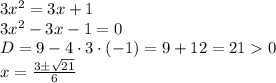
Получили два корня уравнения.
Обе функции определены при данных значениях х, т.е. для обоих значений х существует значение у для обеих функций, а следовательно, и общих точек пересечения - две.
x - pi/6=arctg1/корень из 3 + pin
х= pi/6 + pi/6 + pin
x=pi/3+pin,где n принадлежит Z