
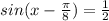

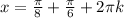
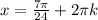
В решении.
Объяснение:
Формула, при которой можно построить уравнение прямой по двум точкам:
(х-х₁)/(х₂-х₁)=(у-у₁)/(у₂-у₁)
Определить координаты двух точек:
точка 1 (-2; 3) - слева вверху, во 2 четверти.
точка 2 (2; -3) - справа внизу, в 4 четверти.
х₁ = -2; у₁ = 3;
х₂ = 2; у₂ = -3.
Подставить данные в формулу:
(х - (-2))/(2 - (-2)) = (у - 3)/((-3) - 3)
(х + 2)/4 = (у - 3)/(-6)
Перемножить крест-накрест, как в пропорции:
-6(х + 2) = 4(у - 3)
-6х - 12 = 4у - 12
-4у = 6х
у = 6х/-4
у = -1,5х - искомое уравнение.
k = -1,5; m = 0.
Запишем уравнение кривой в виде -4*(x²-4*x)+25*(y²+4*y)-16=0, или -4*[(x-2)²-4]+25*[(y+2)²-4]-16=0, или -4*(x-2)²+25*(y+2)²=100, или -(x-2)²/25+(y+2)²/4=1. Это есть уравнение гиперболы с центром симметрии в точке (2;-2), вещественной полуосью a=√25=5 и мнимой полуосью b=√4=2. Вершины гиперболы в данном случае лежат на прямой x=2, параллельной оси ординат. Одни из вершин имеет координаты (2;3), другая - координаты (2;-7). Асимптоты гиперболы задаются уравнениями y-y0=b/a*(x-x0) и y-y0=-b/a*(x-x0), где x0 и y0 - координаты центра симметрии. В нашем случае x0=2, y0=-2, a=5,b=2, поэтому уравнения асимптот принимают вид: y+2=2/5*(x-2) и y+2=-2/5*(x-2).
sin(x-pi/8)=1/2
x-pi/8=(-1)^n*pi/6+pi*n
x=(-1)^n*pi/6+pi/8+pi*n