Найдите сумму пяти первых членов геометрической прогрессии, если b₅ = 81 и b₃ = 36.
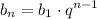
Тогда:
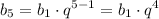
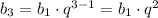
b₅ = b₃ * q²
81 = 36 * q²
q² = 81/36
q = ± √(81/36)
q = ± 3/2 = ± 1,5
b₁ = b₃/q² = 36 : (9/4) = 36 × 4/9 = 16
Формула суммы первых n членов геометрической прогрессии:
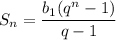
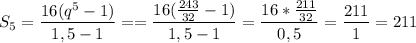
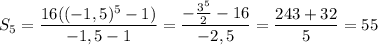
ответ: 211 и 55
S₅=55 или S₅=211
Объяснение:
Формула нахождения n-члена геометрической прогрессии через первый член 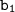 и знаменатель q имеет вид:
и знаменатель q имеет вид:
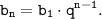
Тогда из 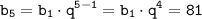 и
и 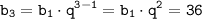 получим:
получим:
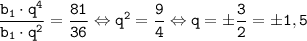 и
и
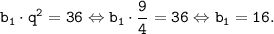
Формула суммы первых n-членов геометрической прогрессии через первый член 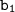 и знаменатель q имеет вид:
и знаменатель q имеет вид:
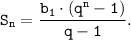
На основе известных данных получим.
a) q=-1,5:
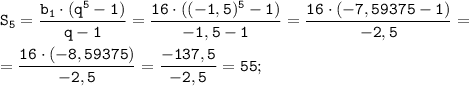
b) q= 1,5:
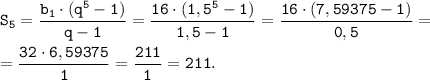
1) Подставить значения а можно сразу.
10а²=10*9²=810.
1. 9²=9*9=81.
2. 10*81=810.
10а²=10*(-0.5)²=10*(-0.5)*(-0.5)=10*0.25=2.5
10а²=10*(-1.2)²=10*(-1.2)*(-1.2)=10*1,44=14,4.
1-ое действие - возведение в степень. Потом умножение.
При умножении двух чисел одинаковых знаков знак произведения "+".
2) Для более лёгкого счёт вынесем общий множитель.
х³-х²=х²(х-1)
Единица, т.к. выносим общий множитель х². х²/х²=1.
Подставляем значения х.
0.3²(0.3-1)= -0.063
1. 0.3-1= -0.7 (из большего модуля вычитаем меньший, ставим знак большего по модулю числа)
2. 0.3²=0.3*0.3=0.09.
3. 0.09*(-0.7)= -0.063 (множители разных знаков - произведение со знаком "-")
Сначала действия в скобках, потом возведение в степень. Уже в конце месяца получившиеся числа.
(-6)²(-6-1)=(-6)*(-6)*(-7)=36*(-7)= -252.
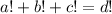 . Будем считать, что
. Будем считать, что 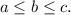
1-й случай. 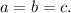 Разделив уравнение на
Разделив уравнение на 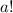 , получаем
, получаем 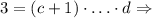 в правой части на самом деле один множитель;
в правой части на самом деле один множитель; 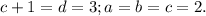 Проверка:
Проверка: 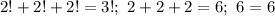 - верно. Итак, одно решение найдено.
- верно. Итак, одно решение найдено.
2-й случай. 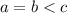 . Разделив уравнение на
. Разделив уравнение на 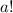 , получаем
, получаем 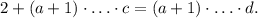 Следовательно,
Следовательно, 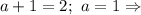 уравнение имеет вид
уравнение имеет вид 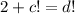 Но два факториала не могут отличаться на 2, поэтому в этом случае уравнение решений не имеет.
Но два факториала не могут отличаться на 2, поэтому в этом случае уравнение решений не имеет.
3-й случай. 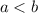 . Разделив уравнение на
. Разделив уравнение на 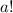 , получаем
, получаем 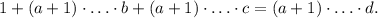 Такое уравнение не может иметь решений, так как все слагаемые, кроме первого, делятся на a+1.
Такое уравнение не может иметь решений, так как все слагаемые, кроме первого, делятся на a+1.
ответ: a=b=c=2; d=3
Найти:
Решение:
Вычислим знаменатель геометрической прогрессии:
Первый член геометрической прогрессии можно вычислить так:
Cумма первых
Вычислим сумму первых
1) Для
2) Для