По задаче не понятно, т.к здесь только описываеться Два отца с их сыновьями)
Пусть  км/ч - это скорость моторной лодки.
км/ч - это скорость моторной лодки.
__________________________________________
 , км/ч
, км/ч 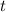 , ч
, ч 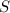 , км
, км
По течению: 

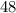
Против течения: 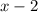
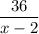
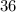
__________________________________________
Так как, по условию, пути в 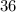 км и
км и 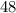 км (против течения и по течению соответственно) были преодолены за одинаковое время, то имеем равенство двух промежутков времени (
км (против течения и по течению соответственно) были преодолены за одинаковое время, то имеем равенство двух промежутков времени (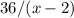 и
и 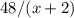 ) вместе с уравнением:
) вместе с уравнением:
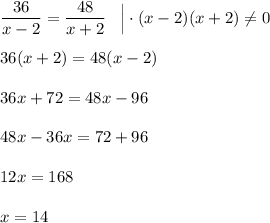
Значит, скорость моторной лодки - 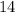 км/ч.
км/ч.
Задача решена!
ответ: 14 км/ч.Моторная лодка за одно и тоже время может проплыть 48 км по течению и 36 км против течения реки. Какова собственная скорость лодки, если скорость течения 2 км\час.
Пусть собственная скорость лодки - х км/ч. Тогда:
По течению: (x + 2) км/ч
Против: (x - 2) км/ч
Из формулы времени:
 , где S - пройденный путь, а v - скорость имеем:
, где S - пройденный путь, а v - скорость имеем:
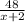 (ч) - время движения по течению
(ч) - время движения по течению
 (ч) - время движения против него
(ч) - время движения против него
Так как время одно и тоже можем составить следующее уравнение:

48(x - 2) = 36(x + 2)
48x - 36x = 96 + 72
12x = 168
x = 14
Значит, собственная скорость лодки 14 км/ч
ответ: 14 км/ч
Ну, очевидно (других имён нет!), что отца Вани зовут Коля.
Проверим нашу догадку.
Итак, Коля дед, Ваня - отец и ещё есть, допустим, Петя - сын Вани и внук Коли.
Пусть Петя поймал х рыб, его отец Ваня - стоко же. т.е. х рыб, а Отец Вани, Коля поймал 3х рыб.
Всего: х + х + 3х = 5х, что по условию равно 35.
5х = 35
х = 7.
Итак, Петя(внук) поймал 7 рыб, Ваня (отец) поймал 7 рыб, а Коля (дед) поймал 21 рыбу.
ответ: Отца Вани зовут Коля