≈ 24,6°
Объяснение:
Для начала найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az}
AB = {3 - 3; -2 - (-1); 2 - (-3)}
AB = {0; -1; 5}
CD = {Dx - Cx; Dy - Cy; Dz - Cz}
CD = {1 - 2; 2 - (-2); 2 - 3}
CD = {-1; 4; -1}
Теперь найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy + ABz · CDz
AB · CD = 0 · (-1) + (-1) · 4 + 5 · (-1)
AB · CD = 0 - 4 - 5
AB · CD = -9
Затем найдем длины векторов:
|AB| =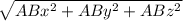 
|AB| =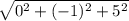 
|AB| =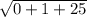 
|AB| =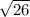 
|CD| =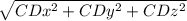 
|CD| =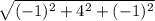 
|CD| =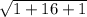 
|CD| =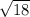 
|CD| = 3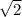
Найдем косинус угла между векторами:
cos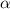 
= 
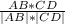
cos =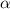 
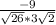
cos =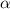 
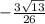
cos 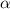= ≈ -0.41602514716892186
И наконец-то находим по таблице брадисса угол, с найденого косинуса
Это ≈ 24,6°
Сделаем замену переменной: у = 2^х. Тогда уравнение перепишется в виде (k - 1) * y^2 - 4y + (k + 2) = 0. Найдем четверть дискриминанта:
D/4 = 4 - (k - 1)(k + 2) = -k^2 - k + 6.
Если уравнение имеет один или более корней, то дискриминант должен быть неотрицательным. Имеем неравенство -k^2 - k + 6 >= 0, отсюда -3 <= k <= 2.
Находим корни:
y1 = (2 + √(-k^2 - k + 6))/(k - 1);
y2 = (2 - √(-k^2 - k + 6))/(k - 1).
Необходимо, чтобы хотя бы один из корней был положительным, иначе уравнение у = 2^x не имеет корней. Имеем два неравенства:
1. 2 + √(-k^2 - k + 6))/(k - 1) > 0;
2. 2 - √(-k^2 - k + 6))/(k - 1) > 0.
Решение первого очевидно: 1 < k <= 2.
Со вторым придется повозиться и разбить его на две системы:
1. 0 < √(-k^2 - k + 6) < 2 и k - 1 > 0.
2. √(-k^2 - k + 6) > 2 и k - 1 < 0.
Решение первой системы: -3 <= k < -2 и 1 < k <= 2.
Решение второй системы: -2 < k < 1.
Решение неравенства - объединение двух промежутков. Значит ответ: -3 <= k < -2 и -2 < k <= 2.