По построению треугольник АBH прямоугольный , следовательно угол Н= 90 градусов,угол А= 60 по условию, угол В= 30 по условию, что сумма углов треугольника равна 180 градусов. Так как ВА является гипотенузой и по условию равна 8 см, можно найти катеты треугольника : ВН=ВА*cos30 или ВН=ВА*sin60 ,а катет АН=AB*sin30 или AH=AB*cos60
ВН=8*cos30=8*0,86=6,88 см
АН=8*sin30=8*0,5=4 см
так как по условию АН=АD=4 cм, тогда АD=8 cм, а так как трапеция прямоугольная и ВН-высота, то DH=CB= 4 cм
площадь трапеции равна S= (a+b): 2 * h= (4+8):2*6.88=41,28 см2
Площадь трапеции равна 41,28 см2
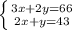
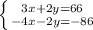
1) Если x = -2, то -16 - 7 = -6 + n, - 23 + 6 = n, n = - 17
2) Если х = -0,2, то -1.6 - 7 = -0.6 + n, -8.6 +0.6 = n, n = -8
3)Если х = 0,4, то 3.2 - 7 = 1.2 + n, -3.8 - 1.2 = n, n = -5
4) Если х = 3, то 24 - 7 = 9 + n, n= 8
№874
Имеет ли уравнение корни при данных значениях n? Если да, то сколько?
1) 2,3y - 6 = 1,8 - 1,7y + n при n=4,2
2,3y - 6 = 1,8 - 1,7y + 4,2
2,3y + 1.7y = 4.2 + 1.8 + 6
4y = 12
y = 3
ответ: да, имеет, у=3
2) 1,5y + 9 + 1/6y= 5/3 + n при n=10
1,5y + 1/6y = 5/3 + 10 -9
3/2y + 1/6y = 2/3
10/6y = 2/3
y = 2/5