 ;
;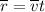 ;
;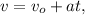 либо в векторном виде:
либо в векторном виде: 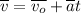 ;
;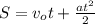 либо в векторном виде:
либо в векторном виде: 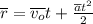 ;
;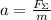 либо в векторном виде:
либо в векторном виде: 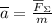 ;
; ;
;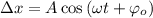 ;
;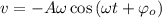 ;
; ;
;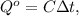 где
где 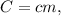 либо в удельном виде:
либо в удельном виде:  ;
;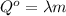 ;
;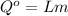 ;
; ;
; ;
;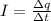 ;
;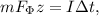 где
где  ;
;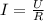 ;
;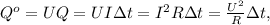
 ;
;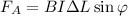 ;
; ;
;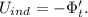
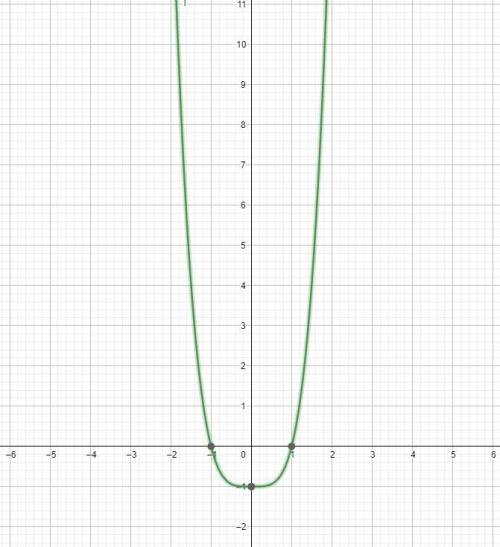
Объяснение:
Для начала найдем область определения функции, и ее потенциальные точки разрыва
1)D(f)=R, точек разрыва нет
2) проверим функцию на четность, очевидно функция четная, т.к. при подстановке вместо икс минус икс функция вида не изменит.
3) найдем нули функции и знак функции на полученных интервалах, для этого разложим функцию на составляющие x^4-1=(x^2-1)(x^2+1)=(x-1)(x+1)(x^2+1)
Приравняем это к нулю, тогда x=1 x=-1
Исследуем знак функции на промежутках от минус бесконечности до минус 1, от минус 1 до 1, и от 1 до +бесконечности. Для этого подставим любую точку из промежутков и получим знаки +-+ (значит на промежутке от -беск до -1 и от 1 до+беск, функция выше оси Ох, на промежутке -1 до 1 функция ниже оси Ох)
приравняв к нулю икс, получим игрик равный -1
4)найдем ассимптоты, так как точек разрыва нет, то и вертикальных ассимптот нет, найдем наклонную асимптоту, для этого вычислим предел
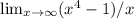 стремится к бесконечности, а значит ассимптот нет
стремится к бесконечности, а значит ассимптот нет
5)Исследуем точки экстремума и интервалы монотонности, тогда найдем производную
4x³ и приравняем ее к нулю 4x³=0, откуда x=0. Найдем знаки слева и справа от нуля, слева минус справа плюс, значит слева от нуля функция убывает, а справа возрастает. Т.к. 0 принадлежит области определения функция, то подставим его в изначальное уравнение, получим -1. Точка (0,-1) - точка экстремума, т.к. в этой точке производная меняет знак с минуса на плюс, то это точка минимума
6) найдем точки перегиба. Для этого найдем вторую производную - производную от производной = 12x^2. приравняем к нулю и вновь получим 0, найдем знаки слева и справа, с обеих сторон +, значит функция выпукла вниз на всей области определения, и точка 0 не является точкой перегиба
7) нужно построить график по всем значениям которые мы получили
BH= КОРЕНЬ ((2КОРНЯ из 3)^2 - (корень из 3)^2)=корень из (12-3)=корень из 9 =3см
AD= корень из 3 + корень из 3 + 2корня из 3 = 4корня из 3 (см)