ОДЗ :
x² - 15 > 0
(x - √15)(x + √15) > 0
+ - +
__________₀______________₀__________
- √15 √15
/////////////////////// ////////////////////////
x ∈ (- ∞ ; - √15) ∪ (√15 ; + ∞)
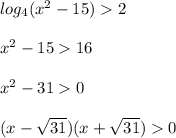
+ - +
____________₀___________₀___________
- √31 √31
////////////////////////// /////////////////////
ответ : x ∈ (- ∞ ; - √31) ∪ (√31 ; + ∞)
Объяснение:
Рассмотрим основные свойства данной функции, которые нам при поиске ответов.
Нули функции, f(x)=0, x²-4x+3=0, x1=1, x2=3.
a=1, ветви параболы направлены вверх.
Минимальное значение f(x) принимает в точке xmin = (x1+x2)/2 = 2.
f(2) = -1.
1. Область определения (-∞; +∞).
2. Область значений [-1; +∞).
3. Минимальное значение f(x) принимает в точке xmin = 2, f(2) = -1.
4. Ось симметрии x=2.
5. Нули функции x1=1, x2=3.
6. f(x)>0, при х∈(-∞;1)∪(3;+∞).
f(x)<0, при х∈(1;3).
7. f(x) убывает при х∈(-∞;2), f(x) возрастает при х∈(2;+∞).
Меняем неизвестное:
Трансформируем функцию:
Строим график функции на координатной сетке
Обратная трансформация (теперь уже координатной сетки):
Сдвигаем координатную сетку на 2 влевоо (график функции уходит на 2 вправо) и получаем график параболы на координатной сетке