1. Обратно пропорциональная зависимость :
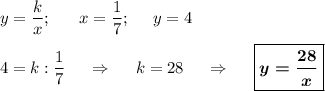
2. Решите графически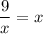 
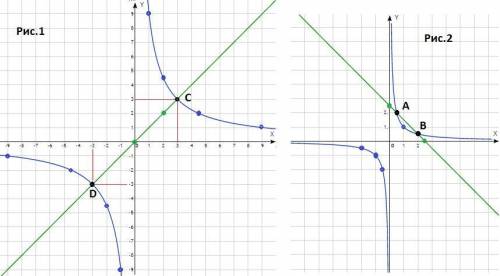
График функции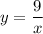 
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
График функции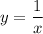 
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.
х∈(3, 4).
Объяснение:
Решить систему неравенств:
х>3
4-х>0
Первое неравенство:
х>3
Решения неравенства находятся в интервале от х=3 до + бесконечности.
х∈(3, +∞), это решение первого неравенства.
Неравенство строгое, скобки круглые.
Второе неравенство:
4-х>0
-x>-4
x<4 знак меняется
Решения неравенства находятся в интервале при х от - бесконечности до 4.
х∈(-∞, 4), это решение второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить оба интервала, чтобы найти пересечение, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем точки 3 и 4. Штриховка от точки 3 вправо до + бесконечности, от 4 влево до - бесконечности.
Пересечение х∈(3, 4), это и есть решение системы неравенств.
!x^2-4x!<3x- модуль эквивалентен системе 2х уравнений
{x^2-4X<3x
{x^2-4x>-3x
РЕшаем каждое отдельно
1. x^2-4x<3x
x^2-4x-3x=0
x^2-7x=0
x(x-7)=0
x=0
x-7=0
x=7
чтобы выражение было отрицательным необходимо чтобы знаки выражения x-7 и x за скобкой отличались, при x<0 знаки совпадают и выражение становится >0,
значит выбираем x из интервала 0<x<7
2. x^2-4x>-3x
x^2-4x+3x=0
x(x-1)=0
x=0 или
x=1
также смотрим и видим что чтобы выражение было положительным надо чтобы знаки за скобкой и в скобке совпадали и выбираем исходя из этого x<0 и x>1
Теперь решением модуля будут те числа которые удоволетворяют пунктам 1 и 2 одновременно, а именно 1<x<7