1.
А множество натуральных
Б кольцо целых
В множество натуральных
Г поле рациональных
2.
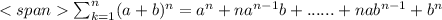
Каждое слагаемое в скобках содержится в правой части тождества в степени ниже чем 1 ровно 1 раз.
То есть все слагаемые,кроме последних после раскрытия исходных скобок будут кратны 10 и заканчиваться на 0.произведение 
будет определять цифру,на которую оканчивается произведение исходных чисел.
Число 6 в любой натуральной степени оканчивается на 6,1 в любой степени даст 1.Произведение равно 6.
Это и есть цифра на которую оканчивается исходное произведение.
применим теорему Виета, x1 x2 x3 корни многочлена a1x^2+a2x^2+a3x+a4
x1+x2+x3=-a2/a1
x1*x2+x2*x3+x1*x3=a3/a1
x1*x2*x3=-a4/a1
подставляем
x1+x2+x3=3
x1*x2+x2*x3+x1*x3=-9
x1*x2*x3=1