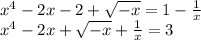
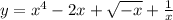 . Каждая из функций
. Каждая из функций 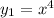 ,
, 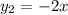 ,
, 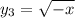 ,
, 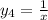 является убывающей на интервале x<0, тогда и сумма этих функций будет убывающей. Монотонная функция если и достигает какого-либо значения, то достигает его только в одной точке. То есть, если заданное уравнение и имеет корень, то он будет единственный. Обычно начинают проверять числа 0 или 1, но здесь они не подходят по ОДЗ. Проверим число x=-1:
является убывающей на интервале x<0, тогда и сумма этих функций будет убывающей. Монотонная функция если и достигает какого-либо значения, то достигает его только в одной точке. То есть, если заданное уравнение и имеет корень, то он будет единственный. Обычно начинают проверять числа 0 или 1, но здесь они не подходят по ОДЗ. Проверим число x=-1: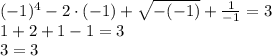
(1-100)(1+100)+(2-99)(2+99)+...+(49-52)(49+52)+(50-51)(50+51)=
= -99*101-97*101-...-1*101 - {50 слагаемых, кратных 101}
Выносим -101 как общий множитель:
-101(99+97+...+3+1)
так же складываем эти слагаемые первое с последним, второе с предпоследним и т.д.: -101(100+100+...+100) - {100 повторяется 25 раз( 50/2}
Получается: -101*100*25= -252500