Первая. Пусть а и b - две разные ненулевые данные цифры (двузначные числа не могут начинаться с 0). Тогда числа образованные с их пощью 10а+в (двузначное число в котором цифра а - количевство десятков, b - количевство единиц), 10a+a, 10b+a, 10b+b. Их сумма
10a+b+10a+a+10b+a+10b+b=22a+22b=22(a+b)=2*11 (a+b)
так как числа 2 и 11 взаимно простые, а сумма должна быть квадратом, то второй ненулевой множитель a+b должен делится на 22, что невозможно так как a и b - цифры, то их сумма не превышает 9+9=18
Таким образом сумма четырех различных двузначных чилес, записанных с двух заданных цифр не может быть квадратом натурального числа. Доказано
Вторая. х^2+5y^2+4xy+2y+1=0
x^2+4xy+4y^2+y^2+2y+1=0
(x+2y)^2+(y+1)^2=0
так как квадрат любого выражения неотрицателен, сумма двух неотрицательных неотрицательное и равно 0, только если каждое из слагаемых равно 0, то
x+2y=0
y+1=0
y=-1
x=-2y=-2*(-1)=2
ответ: (2;-1)
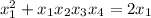
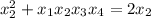
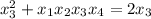

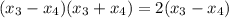

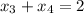
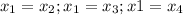
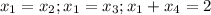
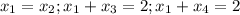
.