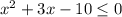
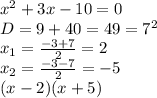
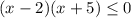
![x \in [-5;2]](/tpl/images/0848/6310/8e377.png)
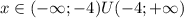
![x \in [-5;-4)U(-4;2]](/tpl/images/0848/6310/15abb.png)
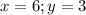
Объяснение:
Данную систему уравнений можно решить банальным методом подстановки, из одного уравнения вычленяя переменную x или y и подставляя ее во второе уравнение.
Но есть и другие решения, я покажу как решить данную систему уравнений методом исключения переменных, что на мой взгляд, гораздо проще с данной системой.
Запишем систему уравнений:
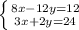
Мы можем избавиться от переменной y. Для этого умножаем и правую, и левую части второго уравнения на 6:
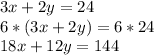
Теперь исключаем переменную y путём сложения двух уравнений. Для начала прибавим второе уравнение системы к первому:
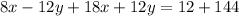
Так как сумма двух противоположных величин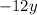 
и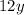 
равна нулю, удаляем их из нашего выражения:
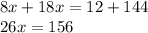
Теперь мы легко получаем значение x из данного уравнения:
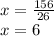
Теперь нам осталось подставить данное значение x во второе уравнение системы:
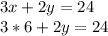
Находим y:
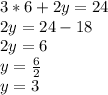
Получили ответ: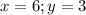
a=0, b=2, c=-6
подставляем:
0x+2y-6=0
2y-6=0
2y=6
y=3
это прямая параллельная оси ОХ, проходящая через точку (0;3)
отмечаешь точку (0;3) и, например, (2;3)
и просто проводишь через их прямую