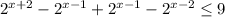
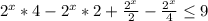
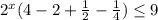
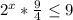

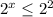
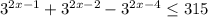
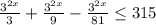
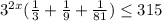

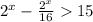
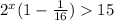
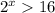
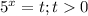
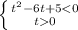
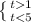
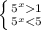
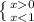
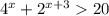
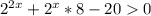
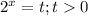
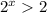

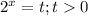
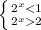
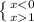
Пусть abc - искомое число.
Найдем все возможные комбинации цифр a, b и c, такие, что S = a + b + c = 21.
Если одна из цифр числа меньше 2, то и S < 2 + 9 + 9 = 21, что не подходит по условию. Таким образом, все цифры числа должны быть больше 2.
Последовательно рассмотрев случаи для семи возможных значений a: a = 3,4,5,6,7,8,9, находим соответствующие им b и c.
С точностью до перестановки цифр, возможных "уникальных" комбинаций всего 7: (3,9,9), (4,8,9), (5,7,9), (5,8,8), (6,6,9), (6,7,8) и (7,7,7).
Комбинации, полученные перестановкой цифр в каждой из этих 7-и комбинаций, представляют различные между собой числа, и также нам подходят. Проделав всевозможные перестановки цифр в каждой тройке, мы найдем все различные n = 28 чисел.
Общее количество трехзначных чисел (т.е. чисел 100, 101, 102, 103, ..., 999), как легко подсчитать, будет N = 999 - 100 + 1 = 900. Откуда и получим искомую вероятность p = 28/900 = 7/225 = 0,03(1).
9+9+0=18 (990, 909 - два числа)
9+8+1=18 (шесть чисел 981, 918, 819, 891, 189, 198)
9+7+2 (шесть чисел)
9+6+3 (шесть чисел)
9+5+4 (шесть чисел)
8+8+2 (288, 828, 882 - три числа)
8+7+3 (шесть чисел)
8+6+4 (шесть чисел)
8+5+5 (три числа)
7+7+4 (три числа)
7+6+5 (шесть чисел)
6+6+6 (одно число)
трехзначных чисел - 54 , сумма которых равна 18
первое трехзначное число 100, последнее 999
999=100+(n-1)*1
999-100=n-1
899=n-1
n=900
всех трехзначных чисел 900
по\тому искомая вероятность равна 54/900=0.06
2^х*2^2 - 2^х*2 + 2^х/2 - 2^х/2^2<=9
2^х(4-2+1/2-1/4)<=9
2^х * 2 1/4<=9
2^х<=4
2^х<=2^2
х<=2