1)
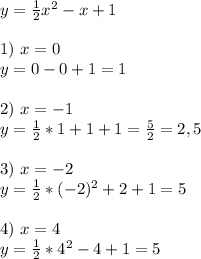
2)
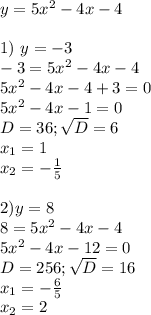
3)
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
5)
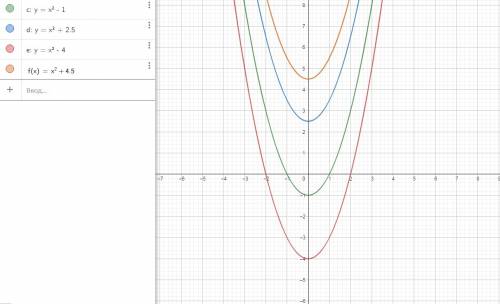
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)
{ (xy)²+3y=45
{ 5y-2xy=3
Замена: xy = t
{ (t)²+3y=45
{ 5y-2t=3 => t= (5y-3) /2 (подставим значение t в первое ур-ние)
((5y-3) /2 )²+3y=45
(5y-3)²/4 +3y=45 | *4
(5y-3)² + 12y= 180
25y² - 30y + 9 + 12y - 180 = 0
25y² - 18y - 171 = 0
D = 324 + 4*25*171 = 324 + 17100 = 17424
√D = 132
y₁= (18 +132) /2*25 = 150/50 = 3
y₂= (1818 - 132) /2*25 = -114/50 = -2,28
Подставим значение y₁ и y₂ в уравнение 5y-2xy=3:
5*3-2x*3=3
х₁ = 2
5*(-2,28) - 2х*(-2,28) = 3
- 11,4 + 4,56х = 3
4,56х = 14,4
х₂ = 3 3/19
ответ: (2;3) , (3 3/19; -2,28)
- х^2 = 11 -2
-x^2 = 9
Если х в условии записан без скобок, то решений нет. Уравнение не имеет действительных значений.
х 2в квадр +3= 3- х
x^2 +x = 3-3
x(x+1) = 0
x =0 x+1 = 0
x =-1
х 2 в квад +2=х+2
x^2 -x = 2-2
x(x-1) = 0
x =0 x-1 = 0
x = 1