Объяснение:
x - количество деталей в 1-й коробке.
y - количество деталей во 2-й коробке.
Система неравенств:
x+y>27; x>27-y
x>2(y-12); x>2y-24
9(x-10)<y; y>9x-90; 9x<y+90; -x>-y/9 -10
x-x>2y-24 -y/9 -10
(18y-y)/9 -34<0
17y<34·9
y<2·9; y<18
При y=17: x>27-17; x>10.
Допустим x=11; y=17:
11+17>27; 28>27
11>2(17-12); 11>10
9(11-10)<17; 9<17
Неравенства выполняются, следовательно, 11 деталей - в 1-й коробке, 17 деталей - во 2-й коробке.
Чтобы сомнений не было, проверим со следующими данными:
x=12; y=16
12+16>27; 28>27
12>2(16-12); 12>8
9(12-10)<16; 18>16 - неравенство не выполняется.
ответ: 11 и 17.
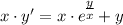
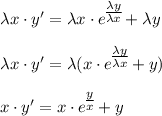
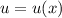с замены:
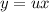, тогда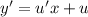 
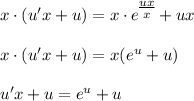
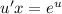
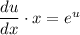- уравнение с разделяющимися переменными.
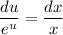- уравнение с разделёнными переменными.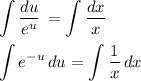
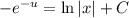- общий интеграл новой функции.
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: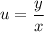 
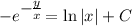- общий интеграл исходного уравнения.
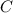. Подставим в общий интеграл начальное условие: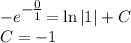
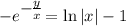- частный интеграл, также является решением данного дифференциального уравнения.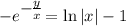
20m^2-5n^4=5·(4m^2-n^4)=5·(2m-n^2)·(2m+n^2)