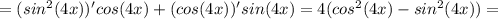
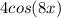
Объяснение:
Систем нету, поэтому решу только две задачи.
1. Купюры на 500 руб, всего 22 штуки.
{ 50x + 10y = 500
{ x + y = 22
Делим 1 уравнение на 10
{ 5x + y = 50
{ x + y = 22
Вычитаем из 1 уравнения 2 уравнение
5x + y - x - y = 50 - 22
4x = 28
x = 7 купюр по 50 рублей.
y = 22 - x = 22 - 7 = 15 купюр по 10 рублей.
2. Прямая y = kx + b; A(5; 0); B(-2; 21)
Подставляем координаты вместо х и у.
{ 0 = k*5 + b
{ 21 = k*(-2) + b
Из 1 уравнения вычитаем 2 уравнение
0 - 21 = 5k + b - (-2)k - b
-21 = 7k
k = -21/7 = -3
b = -5k = -5*(-3) = 15
Прямая y = -3x + 15
Х² + 9х = 0
I.Рациональный решения.
Вынести общий множитель за скобку:
х * (х + 9 ) = 0
Произведение = 0 , если один из множителей =0.
х₁= 0
х + 9=0
х₂= -9
II. Решение через дискриминант [ D= b² -4ac ]
Стандартный вид квадратного уравнения:
х² + 9х + 0 =0
а = 1 ; b= 9 ; с = 0
D = 9² - 4*1*0 = 9²
D>0 - два корня уравнения [ х₁,₂ = (-b ⁺₋ √D)/2a ) ]
х₁ = ( - 9 + √9²) /(2*1) = (-9 + 9)/2 = 0/2 = 0
x₂ = ( - 9 - √9²) /(2*1) = (-9 - 9)/2 = -18/2 = - 9
ответ: ( - 9 ; 0 ) .
Объяснение: