X^2-3x-18/x-6 и второе x^2+10x+21/x^2-9 нужно сократить дробь. ответ на первое x+3 , ответ на второе x+7/x-3

👇

Увидеть ответ

Ответ:

Ariana20199

26.02.2020

1) Разложим числитель дроби на множители

$\sf x^2-3x-18=x^2+3x-6x-18=x(x+3)-6(x+3)=(x-6)(x+3)$

$\sf \dfrac{x^2-3x-18}{x-6}=\dfrac{(x-6)(x+3)}{x-6}=x+3$

2) Аналогично в числителе разложим на множители, а в знаменателе это разность квадратов.

$\sf \dfrac{x^2+10x+21}{x^2-9}=\dfrac{x^2+3x+7x+21}{(x-3)(x+3)}=\dfrac{x(x+3)+7(x+3)}{(x-3)(x+3)}=\dfrac{x+7}{x-3}$

4,4(40 оценок)

Открыть все ответы

Ответ:

vampirka2

26.02.2020

Если 114, то не получается,а если 148, то получается!

Пусть х - собственная скорость катера (или скорость движения по озеру) , у - скорость течения реки

Составим систему уравнений:

4*(х+у) + 3х = 148 - первое уравнение (сложить расстояния, пройденные катером по реке и озеру)

5*(х-у) -2х = 50 - второе уравнение (это разница расстояний, пройденных катером против течения и по озеру за 2 часа)

Раскроем скобки

4х+4у+3х=148

5х-5у-2х=50

будет:

7х+4у=148

3х-5у=50

Из первого уравнения выразим х, и подставим во второе уравнение:

х = (148-4у) /7

3*((148-4у) /7) - 5у = 50

решаем второе уравнение:

(444-12у) /7 - 5у = 50

умножим все части на 7:

444-12у-35у=350

444-47у=350

47у=94

у=2 км/ч - скорость течения реки

х = (148 - 4*2)/7 = 20 км/ч - собственная скорость катера (или скорость в стоячей воде)

Объяснение:

Ну как то так

4,4(91 оценок)

Ответ:

Ok7a

26.02.2020

В обоих случаях нужно делать замену переменной.

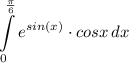
$\displaystyle \int\limits^{\frac{\pi}{6}}_0 {e^{sin(x)}}\cdot cosx \, dx$

Что тут можно предпринять? Известно, 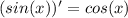(sin(x))' = cos(x) , вот и сделаем замену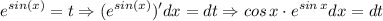 $\displaystyle e^{sin(x)} = t \Rightarrow (e^{sin(x)})'dx=dt \Rightarrow cos\, x\cdot e^{sin \, x} dx=dt$

Вообще идеально, получим простейший интеграл. Так как это определенный интеграл, то обратную замену можно не делать, а просто пересчитать пределы по самой замененной функции

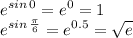
$\displaystyle e^{sin\, 0} = e^0=1 \\ e^{sin \, \frac{\pi}{6}} = e^{0.5}=\sqrt{e}$

То есть пределы станут: 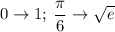$\displaystyle 0 \to 1; \: \frac{\pi}{6} \to \sqrt{e}$

А теперь сам интеграл 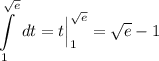$\displaystyle \int\limits^{\sqrt{e}}_1 {} \, dt = t \Big|\limits^{\sqrt{e}}_1 = \sqrt{e} -1$

Теперь следующий интеграл:

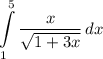
$\displaystyle \int\limits^5_1 {\frac{x}{\sqrt{1+3x}} } \, dx$

Что можно такого заменить? Попробуем взять корень, его производная даст тот же корень в знаменателе, да и сам вполне нормально выражается, делаем:

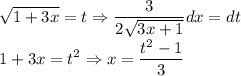
$\displaystyle \sqrt{1+3x}=t \Rightarrow \frac{3}{2\sqrt{3x+1}}dx=dt \\ 1+3x=t^2 \Rightarrow x=\frac{t^2-1}{3}$

Заодно сразу новые пределы посчитаем:

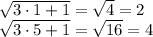
$\sqrt{3\cdot 1+1} = \sqrt{4}=2 \\ \sqrt{3\cdot 5+1} = \sqrt{16}=4$

То есть 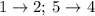$1 \to 2; \: 5 \to 4$

Теперь подставляем и смотрим, что получается:

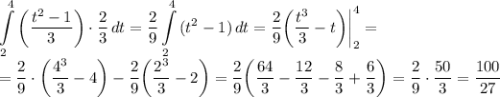
$\displaystyle \int\limits^4_2 {\bigg(\frac{t^2-1}{3} \bigg)\cdot \frac{2}{3} } \, dt=\frac{2}{9}\int\limits^4_2 {(t^2-1)} \, dt =\frac{2}{9}\bigg(\frac{t^3}{3}-t \bigg) \bigg|\limits_2^{4}=\\=\frac{2}{9}\cdot \bigg(\frac{4^3}{3}-4\bigg)-\frac{2}{9}\bigg(\frac{2^3}{3}-2 \bigg)=\frac{2}{9}\bigg(\frac{64}{3}-\frac{12}{3}-\frac{8}{3}+\frac{6}{3} \bigg)=\frac{2}{9}\cdot \frac{50}{3}=\frac{100}{27}$

Можно, конечно, было и получить неопределенный интеграл и в него подставить старые пределы, но пересчет на новые позволяет не совершать часть действий

4,5(1 оценок)

Это интересно:

Стиль-и-уход-за-собой

19.03.2021

Как завивать ресницы: секреты красивого взгляда...

Компьютеры-и-электроника

04.11.2021

Как создавать QR‐коды с помощью Android...

Компьютеры-и-электроника

12.03.2021

Как подготовить кабель Ethernet и объединить два ноутбука в сеть...

Путешествия