По формулам приведения:
если в тригонометрической формуле встречается выражение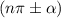 , где
, где 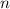 — целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например,
— целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 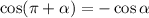 (минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение
(минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение 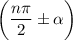 , где
, где 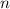 — целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например,
— целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 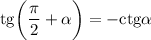 (минус, потому что общий угол будет находиться во второй четверти).
(минус, потому что общий угол будет находиться во второй четверти).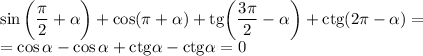
x1+x2=-6
x1=x2+2
2x2=-8
x2=-4
x1x2=q
q=-4*-2=8'
----------------
x^2+px+5=0
x1+x2=-p
x1x2=5
1/x1+1/x2=(x1+x2)/x1x2=-p/5
x1^2+x2^2=(x1+x2)^2-2x1x2=p^2-10
x1/x2+x2/x1=((x1+x2)^2-2x1x2)/x1x2=(p^2-10)/5
x1^3+x2^3=(x1+x2)((x1+x2)^2-3x1x2)=-p(p^2-15)