Алгебра: 1). решите неравенство: 5/6-x 2/3 2). решите уравнение: x^3=4x^2+5x

№1 1) 2) 3) 4) №2 1) Решим уравнение a=1 b=10 c=25 Найдем дискриминант уравнения: Т.к. D=0, то оба корня уравнения будут равны Уравнение имеет два равных корня , соответственно трехчлен можно разложить по формуле: 2) Решим уравнение a=1 b=-14 c=49 Найдем дискриминант уравнения: Т.к. D=0, то оба корня уравнения будут равны Уравнение имеет два равных корня , соответственно трехчлен можно разложить по формуле: 3) Решим уравнение a=1 b=1.8 c=0.81 Найдем дискриминант уравнения: Т.к. D=0, то...

1). решите неравенство: 5/6-x< 2/3 2). решите уравнение: x^3=4x^2+5x

👇

Увидеть ответ

Ответ:

roapoaop

03.07.2020

1) 5/6-x<2/3

-х<2/3-5/6

-x<-1/6

x>1/6

2) x^3=4x^2+5x

-x^3+4x^2+5x=0

x(-x^2+4x+5)=0

x=0 или -x^2+4x+5=0

x^2-4x-5=0

Д=36

x1=5 x2=-1

ответ: 0;5;-1.

4,8(86 оценок)

Открыть все ответы

Ответ:

Aaaaaarrrrr55

03.07.2020

Ядро в алгебре — характеристика отображения f:A– B ,обозначаемая ker f отражающая отличие f от инъективного отображения, обычно — множество прообразов некоторого фиксированного (нулевого, единичного, нейтрального) элемента e. Конкретное определение может различаться, однако для инъективного отображения f множество ker f всегда должно быть тривиально, то есть состоять из одного элемента (как правило, нейтрального элемента из A.

Если множества A и B обладают некоторой структурой (например, являются группами или векторными пространствами), то ker f также должно обладать этой структурой, при этом различные формулировки основной теоремы о гомоморфизме связывают образ Im f и фактормножество A/ker f

4,6(28 оценок)

Ответ:

POLTIT1

03.07.2020

№1
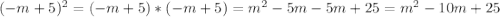
1) $(-m+5)^{2} =(-m+5)*(-m+5)= m^{2} -5m-5m+25=m^{2}-10m+25$
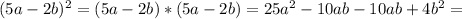
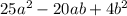
2) $(5a-2b)^{2}= (5a-2b)*(5a-2b)= 25a^{2}-10ab-10ab+4b^{2} =$ $25a^{2}-20ab+4b^{2}$
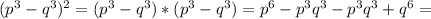
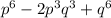
3) $( p^{3}- q^{3} )^{2} =( p^{3}- q^{3} )*( p^{3}- q^{3} )= p^{6}- p^{3} q^{3}-p^{3} q^{3}+ q^{6}=$ $p^{6}- 2p^{3} q^{3}+ q^{6}$
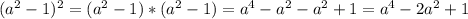
4) $( a^{2} -1)^{2} =( a^{2} -1)*( a^{2} -1)= a^{4} -a^{2}-a^{2}+1=a^{4}-2a^{2}+1$

№2
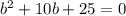
1) Решим уравнение $b^{2} +10b+25=0$
a=1 b=10 c=25
Найдем дискриминант уравнения:
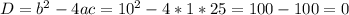
$D= b^{2}-4ac= 10^{2}-4*1*25=100-100=0$
Т.к. D=0, то оба корня уравнения будут равны
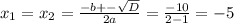
$x_{1}=x_{2}= \frac{-b+- \sqrt{D} }{2a}= \frac{-10}{2-1}=-5$
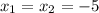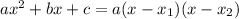
Уравнение имеет два равных корня $x_{1}=x_{2}=-5$ , соответственно трехчлен можно разложить по формуле: $ax^{2}+bx+c=a(x- x_{1} )(x- x_{2})$
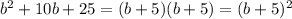
$b^{2} +10b+25=(b+5)(b+5)= (b+5)^{2}$

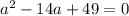
2) Решим уравнение $a^{2} -14a+49=0$
a=1 b=-14 c=49
Найдем дискриминант уравнения:
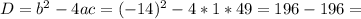
$D= b^{2}-4ac= (-14)^{2}-4*1*49=196-196=$
Т.к. D=0, то оба корня уравнения будут равны
$x_{1}=x_{2}= \frac{-b+- \sqrt{D} }{2a}= \frac{14}{2*1}=7$
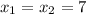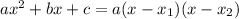
Уравнение имеет два равных корня $x_{1}=x_{2}=7$ , соответственно трехчлен можно разложить по формуле: $ax^{2}+bx+c=a(x- x_{1} )(x- x_{2})$
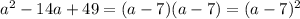
$a^{2} -14a+49=(a-7})(a-7)=(a-7)^{2}$

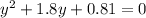
3) Решим уравнение $y^{2} +1.8y+0.81=0$
a=1 b=1.8 c=0.81
Найдем дискриминант уравнения:
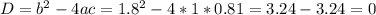
$D= b^{2}-4ac= 1.8^{2}-4*1*0.81=3.24-3.24=0$
Т.к. D=0, то оба корня уравнения будут равны
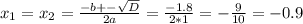
$x_{1}=x_{2}= \frac{-b+- \sqrt{D} }{2a}= \frac{-1.8}{2*1}=- \frac{9}{10}=-0.9$
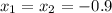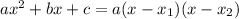
Уравнение имеет два равных корня $x_{1}=x_{2}=-0.9$ , соответственно трехчлен можно разложить по формуле: $ax^{2}+bx+c=a(x- x_{1} )(x- x_{2})$
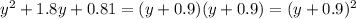
$y^{2} +1.8y+0.81=(y+0.9)(y+0.9)= (y+0.9)^{2}$