В общем виде решение линейного неравенства с одной переменной
можно изобразить так:
1) Неизвестные переносим в одну сторону, известные — в другую с противоположными знаками:
2) Если число перед иксом не равно нулю (a-c≠0), обе части неравенства делим на a-c.
Если a-c>0, знак неравенства не изменяется:
Если a-c<0, знак неравенства изменяется на противоположный:
Если a-c=0, то это — частный случай. Частные случаи решения линейных неравенств рассмотрим отдельно.
Примеры.
Это — линейное неравенство. Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как -2<0, знак неравенства изменяется на противоположный:
Так как неравенство строгое, 10 на числовой прямой отмечаем выколотой точкой. Штриховка от 10 влево, на минус бесконечность.
Так как неравенство строгое и точка выколотая, 10 записываем в ответ с круглой скобкой.
Объяснение:
по определению функция называется возрастающей когда f(x)>f(y) где x>y
вот воспользуемся определением и запишем разность получим выражение что на картинке потом умножим и поделим на сопряженное в верху получилось разность аргументов по условию x(n+1)>x(n) значит наша разность сверху положительная а снизу получилась сумма положительных она тоже положительная а так как вся дробь положительная значит наша разность положительная и f(x+1) больше f(x) можно и писать m и n для большей общности
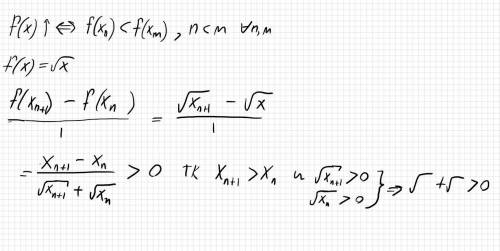
Если в е) синус 3π/2, а не 2π/3.