1)
У=-2х^2+5х+3
-4 =-2х^2+5х+3
-2х^2+5х+7 = 0
D = 25+ 2*7*4 = 25+56 = 81
корень из D = 9
х1 = (-5 +9)/(-4) = -1
х2 = (-5 -9)/(-4) = 3,5
2) (файл прикреплю)
а) y=9/4+3-8=5.25-8= -2.75
б) x^2-2x-11=0
x1=1+2√3
x2=1-2√3;
3) (от -∞ до -2] и [от 4 до +∞)
4) (от -∞ до 1]
3)
ибо ветви направлены вниз, то вершина параболы принимает наибольшее значение.
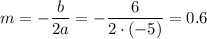
тогда, подставив х=0,6 в заданную функцию, получаем наибольшее значение функции:
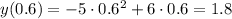
Наименьшего значения функции нет.
как то так наверное....
https://ru-static.z-dn.net/files/d0c/b840827e4223ecccede8572e809f0887.jpg
1)
У=-2х^2+5х+3
-4 =-2х^2+5х+3
-2х^2+5х+7 = 0
D = 25+ 2*7*4 = 25+56 = 81
корень из D = 9
х1 = (-5 +9)/(-4) = -1
х2 = (-5 -9)/(-4) = 3,5
2) (файл прикреплю)
а) y=9/4+3-8=5.25-8= -2.75
б) x^2-2x-11=0
x1=1+2√3
x2=1-2√3;
3) (от -∞ до -2] и [от 4 до +∞)
4) (от -∞ до 1]
3)
ибо ветви направлены вниз, то вершина параболы принимает наибольшее значение.
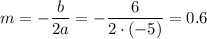
тогда, подставив х=0,6 в заданную функцию, получаем наибольшее значение функции:
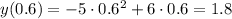
Наименьшего значения функции нет.
как то так наверное....
https://ru-static.z-dn.net/files/d0c/b840827e4223ecccede8572e809f0887.jpg
Зная фoрмулу b_n=b1+q^(n-1)
b2=b1+q^(2-1) или: b1+q=4
b4=b1+q^(4-1) или: b1+q^3=1
Решим систему уравнений:
b1+q=4
b1+q^3=1 для решения данной системы уравнений вычтем из первого уравнения второе уравнение и получим:
q-q^3=3
q(1-q^2)=3
q1=3
q^2=1
q2,3=+-1 И так как у нас убывающая геометрическая прогрессия, так как b4<b1,
то q=-1
Найдём b1: b1-1=4
b1=4+1=5
ответ: b1=5; q=-1