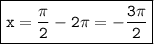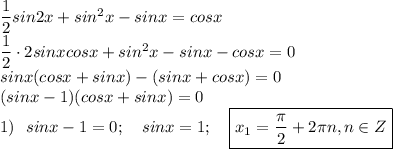
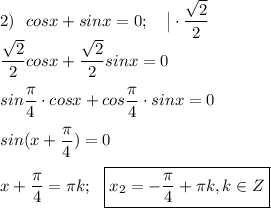
Kорни уравнения на отрезке [-2π;-π/2]. Выбор корней на единичной окружности.
x₁ = -3π/2; x₂ = -5π/4;
![С1 решить уравнение (1/2)sin2x+sin^2x-sinx=cosx и указать корни уравнения на отрезке [-2π; -π/2]](/tpl/images/0231/3404/60ee4.jpg)
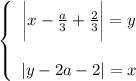
Область определения:
Так как модули неотрицательны, то x ≥ 0 и y ≥ 0
Возможны 4 варианта:
1)
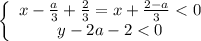
Тогда:
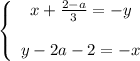
Переносим неизвестные налево, а числа с параметрами направо:
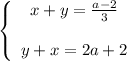
Слева части одинаковые. Если справа будут тоже одинаковые, то получится два одинаковых уравнения, то есть по сути одно.
Оно будет иметь бесконечно много решений, что нам и нужно.
(a - 2)/3 = 2a + 2
a - 2 = 6a + 6
5a = -8
a = -8/5 = -1,6
Подставляем в систему:
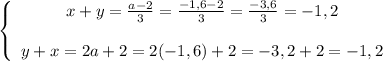
Из условия:
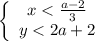
Получаем:
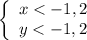
Но по области определений: x ≥ 0; y ≥ 0.
Получили противоречие, значит, в этом варианте решений нет.
2)
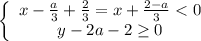
Тогда:
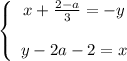
Переносим неизвестные налево, а числа с параметрами направо:
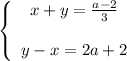
Складываем уравнения и получаем:
2y = (a-2)/3 + 2a + 2 = (a-2+6a+6)/3 = (7a+4)/3
Эта система всегда будет иметь одно решение.
y = (7a+4)/6
x = y - 2a - 2 = (7a+4)/6 - 2a - 2 = (7a+4-12a-12)/6 = -(5a+8)/6
Этот вариант нам не подходит.
3)
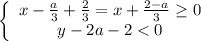
Тогда:
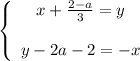
Переносим неизвестные налево, а числа с параметрами направо:
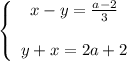
Складываем уравнения и получаем:
2x = (a-2)/3 + 2a + 2 = (a-2+6a+6)/3 = (7a+4)/3
Эта система всегда будет иметь одно решение.
x = (7a+4)/6
y = 2a + 2 - x = 2a + 2 - (7a+4)/6 = (12a+12-7a-4)/6 = (5a+8)/6
Этот вариант нам не подходит.
4)
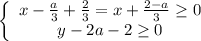
Тогда:
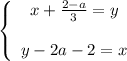
Переносим неизвестные налево, а числа с параметрами направо:
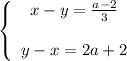
Или по-другому:
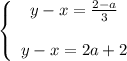
Слева части одинаковые. Если справа будут тоже одинаковые, то получится два одинаковых уравнения, то есть по сути одно.
Оно будет иметь бесконечно много решений, что нам и нужно.
(2 - a)/3 = 2a + 2
2 - a = 6a + 6
7a = -4
a = -4/7
Подставляем в систему:
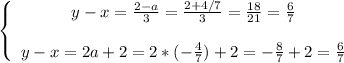
Из условия:
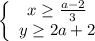
Получаем:
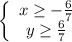
Но по области определения: x ≥ 0
При a = -4/7 будет:
x ∈ [0; +oo); y = x + 6/7 - бесконечно много решений.
Произведение равно нулю, если хотя бы один из множителей равен нулю
При х=π/2 имеет 1=0 - не верно, значит имеем право разделить левую и правую части уравнения (*) на cosx≠0.
Отбор корней на отрезке [-2π;-π/2].
1. Если n=-1, то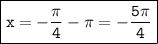
2. Если k=-1, то