Объяснение:
1)(2a - 5b)·(... - ...) = 6a^3 - 15a^2*b - 14ab + ...;
6a^3 : 2a = 3a^2
14ab : 2a = 7b
(2a - 5b)(3a^2 - 7b) = 6a^3 - 15a^2*b - 14ab + 35b^2
2)(... - ...)·(6x^2 - 5y^2) = 12x^3 + 42x^2*y - ... - 35y^3;
12x^3 : 6x^2 = 2x
-35y^3 : (-5y^2) = 7y
(2x + 7y)(6x^2 - 5y^2) = 12x^3 + 42x^2*y - 10xy^2 - 35y^3
3)(3a + 4c)·(... + ...) = 20ac + 8bc + 6ab + ...;
20ac : 4c = 5a
6ab : 3a = 2b
(3a + 4c)(5a + 2b) = 20ac + 8bc + 6ab + 15a^2
4)(... + ...)·(2a + 5b) = ... + 5ab + 8ac + 20b
Здесь опечатка, в конце должно быть 20bc
5ab : 5b = a
8ac : 2a = 4c
(a + 4c)(2a + 5b) = 2a^2 + 5ab + 8ac + 20bc
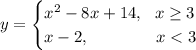
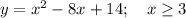
Найдём вершину параболы:
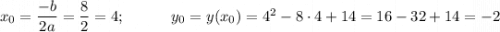
В данной точке можно обозначить опорную прямую, которая будет симметрична для ветвей (тогда значения с одной стороны можно просто симметрично перенести на другую)
Возьмём 3 точки (при ограничении прямой x < 3 даже 3-ёх много будет)
1) x = 5
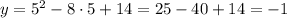
2) x = 6
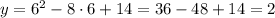
3) x = 7
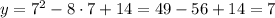
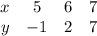
Отмечаем точки на координатной плоскости и симметрично их копируем относительно вс прямой
Не стоит забывать что условие ограничения функции x ≥ 3, поэтому переносим только точку, симметричную B; позже на графике эта точка будет закрашена и обозначена как A
(картинка 1)
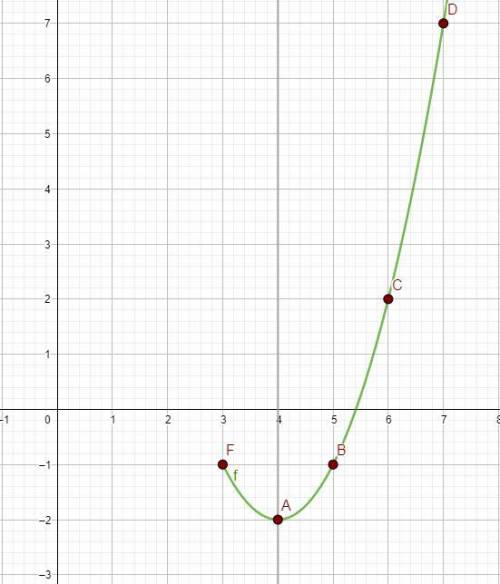
Разбираемся со вторым графиком
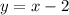
Уравнение прямой, достаточно двух точек
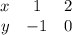
Условие x < 3, точка (3; 1) выколота
(картинка 2)
y = m
При m = 1 (и всё что выше) получаем 1 точку пересечения
Следовательно, подходят все значения до m = 1
При m = -1 и до m = -2 имеем 3 точки пересечения
При m = -2 2 точки пересечения (вершина параболы и прямая)
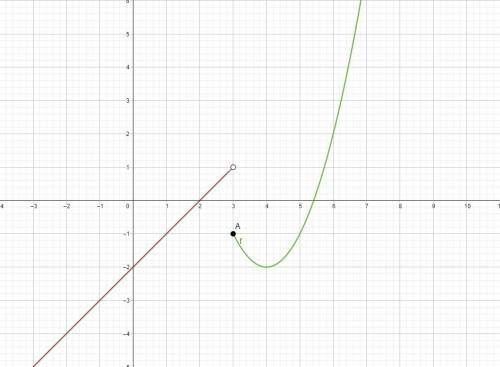
Следовательно нам подходят значения -2; от -1 до 1 не включительно
ответ: 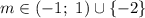
х (х + 3) = 0
Х1 = 0
Х2 = - 3/1 = -3
4х² + 28х + 49 = 0
D = 28² - 4 × 4 × 49 = 784 - 784 = 0
D = 0, будет один корень
Х = - 28/2*4 = - 28/8 = - 3,5
9х² + 6 = 21х
9х² - 21х +6 =0
D = (-21)² - 4 * 9 * 6 = 441 - 216 = 225
Х1 = - (-21) - √225 21 - 15
= = 1/3
2 * 9 18
Х2 = -(-21) + √225 21 + 15
= = 36/18 = 2
2 * 9 18
3х² - 8 +10х = 0
3х² + 10х - 8 =0
D = 10² - 4 * 3 * (-8) = 100 + 96 = 196
Х1 = -10 - √196 - 10 - 14
= = - 24/6 = - 4
2 * 3 6
Х2 = - 10 + √196 - 10 + 14
= = 2/3
2 * 3 6
14 + 5х² - 10х = 0
5х² - 10х + 14 = 0
D + (-10)² - 4 * 5 * 14 = 100 - 280 = - 180
D < 0 корней нет
5х - х² = 0
-х² + 5х = 0
х² - 5х = 0
Х1 = 0
Х2 = - (-5/1) = 5
169 - b² = 0
- b² + 169 = 0
b² - 169 = 0
(b - √169/1) (b + √169/1) = Х1,2 = + - 14