S1=80 cм2
S2=245 см2
Объяснение:
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Коэффициент подобия k=4/7, но нам неизвестна площадь ни одного треугольника, а известна только сумма площадей S1+S2=325.
Обозначим:
S1 - площадь первого треугольника
325-S1=S2 - площадь второго треугольника
Составим отношение:
S1/(325-S1)=(4/7)^2
Возводим в квадрат дробь справа:
S1/(325-S1)=16/49
По правилу креста:
S1*49=16*(325-S1)
49*S1=5200-16*S1
49*S1+16*S1=5200
65*S1=5200
S1=5200:65
S1=80 cм2
Площадь второго треугольника 325-S1=325-80=245 см2
№6
3х – 5 (2х + 1) = 3 ( 3 – 2х)
3х–10х–5=9–6х
3х–10х+6х=9+5
–х=14
х=–14
ответ: –14
№5
х²–3х–3у–у²= –3(х+у)+х²–у²= –3(х+у)+(х+у)(х–у)= (х+у)(–3+х–у)
№1
(а +6)²–2а(3 – 2а)=а²+12а+36–6а+4а²= 5а²+6а+36
№2
Система:
5х – 2у = 11
4х – у = 4 |*(–2)
Система:
5х – 2у = 11 (Ур 1)
–8х+2у=–8 (Ур 2)
Сложим уравнения 1 и 2, получим:
–3х=3
х=–1
Подставим значение х у уравнение 1, получим:
5*(–1)–2у=11
–5–2у=11
–2у=16
у=–8
ответ: х=–1; у=–8
№4
Пусть х км– путь в третий день, тогда во второй х+5, а в первый (х+5)+10
Составим уравнение:
х+(х+5)+(х+5+10)=50
х+х+5+х+5+10=50
3х=50–10–5–5
3х=30
х=10
Тогда в третий день 10 км, во второй 10+5=15 км, в первый 10+5+10=25 км
ответ: Первый день 25 км; второй день 15 км; третий день 10 км.
№3
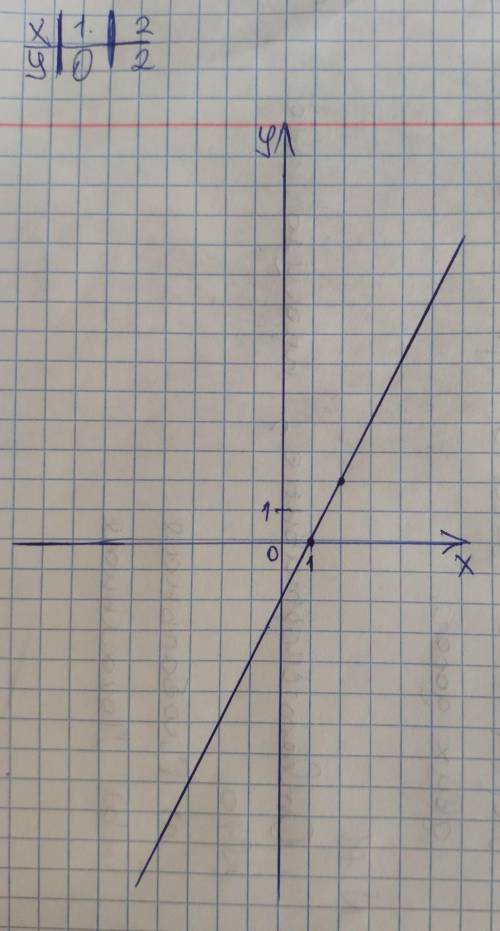
Кординаты точки А х=–10; у=–20.
Подставим значения в функцию у = 2х – 2, получим:
–20=2*(–10)–2
–20=–20–2
–20≠–22
Следовательно график НЕ проходит через точку А.
График во вложении