x∈(0;1/5)∪(25;∞)
Объяснение:
ОДЗ: x>0
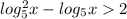 - логарифмическое квадратное неравенство, замена переменной:
- логарифмическое квадратное неравенство, замена переменной:
log₅x=t,
t²-t>2, t²-t-2>0 -метод интервалов:
1. t²-t-2=0, t₁= - 1, t₂= 2
2. + - +
-----------(- 1)-----------(2)---------------->t
3. t<-1, t>2
обратная замена:
1. t<-1, log₅x<-1, log₅x<log₅5⁻¹, log₅x<log₅(1/5)
основание логарифма а=5, 5>1, =. знак неравенства не меняем:
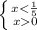
x∈(0; 1/5)
2. t>2, log₅x>2, log₅x.log₅5², log₅x>log₅25
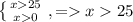
x∈(25;∞)
x∈(0;1/5)∪(25;∞)
с - гипотенуза прямоугольного треугольника, с =37 см, S - его площадь, S=210 см², a и b - катеты.
S = (a*b)/2 = 210
По теореме Пифагора
c² = a² + b²
a² + b² = 37²
ab=420
a=420/b
( 420/b)² + b² = 1369
176400/b² + b² = 1369
b⁴ - 1369b² + 176400 = 0
b²=t > 0
t² - 1369t + 176400 = 0
D = 1369² - 4*176400 =1168561; √D = 1081
t₁ = (1369 + 1081)/2 = 1225; t₂ = (1369 - 1081)/2 = 144
b₁ = √1225 = 35; b₂ = √144= 12;
a₁ = 420/35 = 12; a₂ = 420/12 = 35
35 cм и 12 см