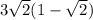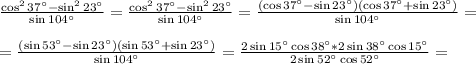
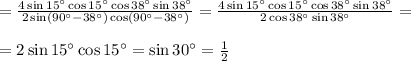
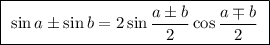
В решении.
Объяснение:
В одній системі координат побудуйте графік функцій і вкажіть координати точок їх перетину y= 2x+1 и y= -x+4.
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = 2x + 1 y = -x + 4
Таблицы:
х -1 0 1 х -1 0 1
у -1 1 3 у 5 4 3
Согласно графиков, координаты точки пересечения прямых (1; 3).
Объяснение:
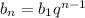 решаем по этой формуле (1)
решаем по этой формуле (1)
q - знаменник
131 - 1) 32 = 108q³ ⇒ q³ = 8/27 ⇒ q = 2/3
131-2) b₃ =  ⇒ q = √5
⇒ q = √5
132. 7-4 = 3 ⇒ c₇ = c₄*q³ ⇒ q³ = -320/40 = -8 ⇒ q = -2 ⇒ c₁ = c₄/q³ = 40/8 = 5
133. b₁ = 3/4, q = 2
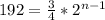

n-1 = 8
n = 9
134. 48, 48q, 48q², 48q³, 243 ⇒ 243 = 48q⁴ ⇒ q⁴ = 243/48 = 81/16 ⇒ q = 3/2 = 1.5
48, 72, 108, 162, 243 вот жирным выделены эти ТРИ числа
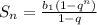 (2)
(2)
135-1) из ф-лы (1): 280= b₁5³ ⇒ b₁ = 280/125 = 56/25
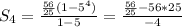
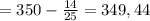
135-2) из формулы (1) 4√2 = q⁴ *√2 ⇒ q = -√2 Т. к. по условию q <0
из (2) 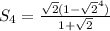
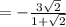 или
или