Объяснение:
Для того, чтобы найти решение системы:
3x + 8y = 13;
5x - 16y = 7,
нам удобнее всего будет применить метод сложения. Рассмотрев оба уравнения мы видим, что перед переменной y в обеих уравнениях мы можем сделать взаимно противоположными коэффициенты.
Умножаем на 2 первое уравнение системы:
6x + 16y = 26;
5x - 16y = 7.
Сложим два уравнения системы:
6x + 5x = 26 + 7;
8y = 13 - 3x;
Решим первое уравнение:
6x + 5x = 33;
11x = 33;
x = 33 : 11;
x = 3.
Система уравнений:
x = 3;
y = (13 - 3 * 3)/8 = (13 - 9)/8 = 4/8 = 1/2.
x = 4; y = 5.
Объяснение:
1) Метод подстановки
решим нижнее уравнение относительно x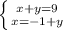 зная значение x из нижнего уравнения, подставим значение x в верхнее уравнение
зная значение x из нижнего уравнения, подставим значение x в верхнее уравнение 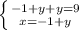 решаем верхнее уравнение как обычное уравнение
решаем верхнее уравнение как обычное уравнение 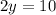 y = 5;Дальше решаем нижнее уравнение как обычное уравнение, зная, что y = 5
y = 5;Дальше решаем нижнее уравнение как обычное уравнение, зная, что y = 5 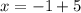 ;x = 4.
;x = 4.2) Метод исключения переменной
сложим два уравнения вместе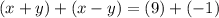 ;решим это уравнение как обычное уравнение
;решим это уравнение как обычное уравнение 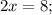 ;x = 4.Подставим значение x в уравнение x+y=9
;x = 4.Подставим значение x в уравнение x+y=9 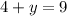 ;y = 5.
;y = 5.3) Метод сравнения
перенесем все y в правые части выражений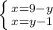 ;зная, что и 9-y и y-1 равны x - сравним их
;зная, что и 9-y и y-1 равны x - сравним их 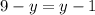 ;решим это уравнение как обычное уравнение
;решим это уравнение как обычное уравнение 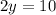 ;y = 5подставляем значение y в выражение x = y-1
;y = 5подставляем значение y в выражение x = y-1 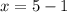 ;x = 4.
;x = 4.Если мой ответ этого заслуживает, отметь его как лучший . Это очень важно для меня
D=4-4×(-3)=4+12=16
_______+_____________-_______________+___________
(возр) -1 (убыв) 3 (возр)
Числа -1 и 3 входят в промежуток [-2; 4]
у наиб=
y наим=