В решении.
Объяснение:
1.
а) b/√7 * √7/√7 = b√7/7;
б) 5/√x *√x/√x = 5√x/x;
в) 5/3√6 *√6/√6 = 5√6/3*6 = 5√6/18;
г) 12/7√2 *√2/√2 = 12√2/7*2 = 12√2/14 = 6√2/7;
д) 1/√3 * √3/√3 = √3/3;
е) 5/4√5 * √5/√5 = 5√5/4*5 = 5√5/20 = √5/4.
2.
а) 2/(√c+y) * (√c+y)/(√c+y) = 2(√c+y)/(c+y);
б) 6/(√5 + 1) * (√5 - 1)/(√5 - 1) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 6(√5 - 1)/(√5)² - 1² =
= 6(√5 - 1)/(5 - 1) =
= 6(√5 - 1)/4 =
= 3(√5 - 1)/2;
в) с/(√a - √c) * (√a + √c)/(√a + √c) =
в знаменателе развёрнутая разность квадратов, свернуть:
= c(√a + √c)/(√a)² - (√c)² =
= c(√a + √c)/(a - c);
г) k/(x + √k) * (x - √k)/(x - √k) =
в знаменателе развёрнутая разность квадратов, свернуть:
= k(x - √k)/(x² - (√k)²) =
= k(x - √k)/(x² - k);
д) 5/(√13 + √3) * (√13 - √3)/(√13 - √3) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 5(√13 - √3)/(√13)² - (√3)² =
= 5(√13 - √3)/(13 - 3) =
= 5(√13 - √3)/10 =
= (√13 - √3)/2;
е) 6/(5 - 2√6) * (5 + 2√6)/(5 + 2√6) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 6(5 + 2√6)/(5² - (2√6)²) =
= 6(5 + 2√6)/(25 - 4*6) =
= 6(5 + 2√6)/1 =
= 6(5 + 2√6).
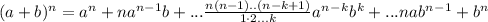
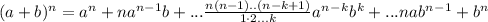
14sin^2(x) + 4cos(2x) = 11sin(2x) - 4.
cos(2x) = cos^2(x)-sin^2(x), подставим:
14sin^2(x) + 4cos^2(x) - 4sin^2(x) = 11sin(2x) - 4.
14sin^2(x) + 4cos^2(x) + 4 - 4sin^2(x) = 11sin(2x)
14sin^2(x) + 4cos^2(x) + 4 (1 - sin^2(x)) = 11sin(2x) (мы использовали, что 1-sin^2(x) = cos^2(x))
14sin^2(x) + 4cos^2(x) + 4 cos^2(x) = 11sin(2x)
14sin^2(x) + 8cos^2(x) - 11sin(2x) = 0;
sin(2x) = 2sin(x)cos(x), подставим:
14sin^2(x) + 8cos^2(x) - 22cos(x)sin(x) = 0; let's divide everything by cos^2(x), знай что sin/cos = tg,
Важно: x не равен Pi/2 + 2Pi*n, где n целое;
14 tg^2(x) + 8 - 22 tg(x) = 0;
обозначим tg(x) as y
14y^2 -22y + 8 = 0
let's simplify a bit
7y^2 - 11y + 4 =0
D = 121 - 112 = 9
y1 = (11 - 9) /14 = 2/14
y2 = (11 + 9) /14 = 18/14
tg(x) = 2/14
or tg(x)= 18/14
x = arctg(2/14) + Pi*k, где k целое
или x = arct(18/14) + Pi*k гдеk целое
ответ:
arctg(2/14) + Pi*k, где k целое
и
arctg(18/14) + Pi*l где l целое