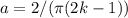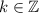, 
, но для них будет всегда больше одного решения, т.к. даже при самом большом значении a при k=0 и k=1 прямая (ax+1)/2 пересечет график cos(x) в трех точках. А значит, при всех остальных а угол наклона прямой будет еще меньше, и, значит, пересечений с косинусом будет еще больше.
f'(x)=(√2*(1-x)+cos 2x)' = √2*(-1) - sin 2x*(2x)'=-√2 -2sin 2x
-√2 - 2 sin 2x = 0
sin 2x = -√2/2
1) 2x = -π/4 + 2πn
x₁ = -π/8 + πn
2) 2x = π-(-π/4) + 2πk
2x = 5π/4 + 2πk
x₂ = 5π/8 + πk
ответ: x₁ = -π/8 + πn; x₂ = 5π/8 + πk; n,k∈Z