Объяснение:
Линейное уравнение – уравнение, сводящееся к виду ax+b=0, где a≠0,b – числа. Линейное уравнение всегда имеет единственное решение x=−ba. Квадратное уравнение – уравнение, сводящееся к виду ax2+bx+c=0, где a≠0,b,c – числа. Выражение D=b2−4ac называется дискриминантом квадратного уравнения. Квадратное уравнение может иметь не более двух корней: ∙ если D>0, то оно имеет два различных корня и x1=−b+D2aиx2=−b−D2a ∙ если D=0, то оно имеет один корень (иногда говорят, что два совпадающих) x1=x2=−b2a ∙ если D<0, то оно не имеет корней. ▸ Теорема Виета для квадратного уравнения: Если квадратное уравнение имеет неотрицательный дискриминант, то сумма корней уравнения x1+x2=−ba а произведение x1⋅x2=ca ▸ Если квадратное уравнение: ∼ имеет два корня x1 и x2, то ax2+bx+c=a(x−x1)(x−x2). ∼ имеет один корень x1 (иногда говорят, что два совпадающих), то ax2+bx+c=a(x−x1)2. ∼ не имеет корней, то квадратный трехчлен ax2+bc+c никогда не может быть равен нулю. Более того, он при всех x строго одного знака: либо положителен, либо отрицателен. ▸ Полезные формулы сокращенного умножения: x2−y2=(x−y)(x+y)(x+y)2=x2+2xy+y2(x−y)2=x2−2xy+y2 Ознакомиться с полной теорией
Если это задача из школьной программы, то ее можно решить так:
О—орел
Р— решка
Возможные варианты при бросании трижды:
1) О О О
2) О О Р
3) О Р О
4) Р О О
5) О Р Р
6) Р Р О
7) Р О Р
8) Р Р Р
Всего 8 исходов
Благоприятных исходов: 3 (выпало ровно две решки)
Вероятность равна: р=3/8=0,375
ответ: 0,375
Если из высшей математики, то лучше по формуле Бернулли:
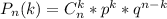
k=2 —количество наступления нужного события
n=3 — количество испытаний
p=0,5 — вероятность наступления события (появление решки)
q=1-p=1-0,5=0,5 — вероятность противоположного события (выпадение орла)
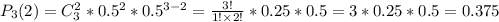
ответ: 0,375
(2a^3+2ab^)-(a^3+2a^b-ab^)+(a^3+2a^b+ab^)
2a^3+2ab^-a^3-2a^b+ab^+a^3+2a^b+ab^
3a^3+4ab^
3*(-1,5)^3+4(-1,5*(-0,25)^)=-10,125-0,375=-10,5