Ну сначала надо это изобразить эту красоту. Очевидно, что шар описан около тетраэда.
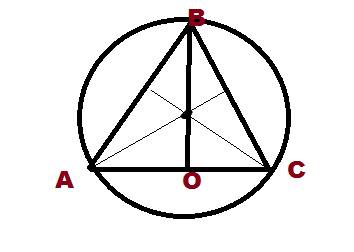
Второй чертеж - наша красота в сечении. То есть рассекаем через центр и вершину тетраэда. Получаем в сечении правильный треугольник, который вписан в круг. (я сделала его во вложении). Если мы построим медианы/высоты/биссекрисы, то они пересекуться в центре круга. По своействам правильного треугольника, его медианы/высоты/биссектрисы делятся точкой пересечения 2к1 от вершины то есть наш радиус это 2/3 от высоты треугольника. Находим высоту. (3√2*3)/2=4,5√2.
Теперь рассмотрим половину нашего треугольника, которую мы отделили высотой (то есть треугольник ОСВ. Угол С=60°, така как правильный треугольник.
sinC=BO/BC=√3/2
BO=4,5√2. BC - искомая сторона
4,5√2/BC=√3/2
4,5√2=√3/2 *ВС
9√2/√3 = ВС
1 ч. 5 мин.=13/12 ч.
Пусть х км/ч - скорость на подъёме, тогда скорость на спуске - (х+2) км/ч. Пусть у км - расстояние от станции до вершины горы, тогда расстояние от вершины горы до озера - (5-у) км. На дорогу от станции до озера рыболов затратил y/x+(5-y)/(x+2) или 1 час; на обратную дорогу - (5-у)/х + у/(х+2) или 1,1 часа. Составим и решим систему уравнений:
Произведём подстановку:
Домножим второе уравнение на 12/25:
По теореме Виета корнями уравнения являются 4 и -1,2. Так как скорость не может быть отрицательным числом, получаем, что скорость на подъёме была равна 4 км/ч, а на спуске 4+2=6 км/ч.
Путь от станции до вершины (4^2-3*4)/2=2 км, от вершины до озера 5-2=3 км.
ответ: скорость на подъёме 4 км/ч, скорость на спуске 6 км/ч.