Для знаходження коренів рівняння 3/x² - 1 = 2/x² + x - 5/x² - x, спочатку приведемо його до спільного знаменника:
3/x² - 1 = 2/x² + x - 5/x² - x
Знаменник у всіх дробах однаковий, тому можемо записати рівняння без знаменника:
3 - x² = 2 + x² - 5 - x² + x² - x
З'єднаємо подібні терміни:
3 - x² = -3 - x
Перенесемо всі терміни на одну сторону:
0 = -6 - x + x²
Перепишемо рівняння в порядку спадання степенів:
x² - x - 6 = 0
Тепер можемо спробувати розкласти це квадратне рівняння на множники або використати квадратну формулу:
(x - 3)(x + 2) = 0
Отже, отримали два корені:
x₁ = 3
x₂ = -2
Таким чином, коренями рівняння є x = 3 та x = -2.
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
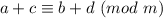
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
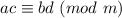
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
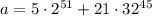
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,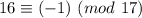 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что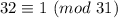 
, получаем
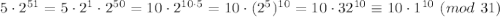
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
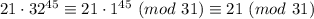
Остаток 21, чудесно. Выполняем последний шаг.
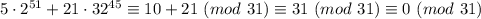
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
