х мальчиков в классе
у девочек в классе
3х/5 мальчиков изучают английский язык
3у/7 девочек изучают английский язык
2х/5 мальчиков изучают немецкий язык
4у/7 девочек изучают немецкий язык
По условию
(3х/5 + 3у/7) > (2х/5 + 4у/7) на 2
Получаем уравнение:
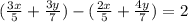
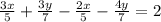
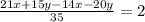
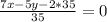
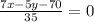
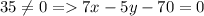
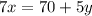
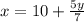
По условию
25 < (x+y) < 36 => (x+y) ∈ (25; 36)
Далее решаем методом подбора.
1) Пусть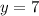 
, тогда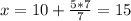 
х=15; у=7
(х+у) = 7+15=22 ∉ (25; 36)
2) Пусть 
, тогда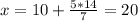 
х=20; у=14
(х+у) = 14+20=34 ∈ (25; 36)
Получаем:
20 мальчиков в классе
14 девочек в классе
20-14 = 6
В классе на 6 мальчиков больше, чем девочек.
ответ под буквой А. Мальчиков, на 6.
Формула для нахождения корней квадратного уравнения
Выражение под знаком корня называется дискриминантом и обычно обозначается буквой D.
Формула для нахождения дискриминанта:
При решении возможны три случая:
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Тогда у квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых. Но, в упрощённом варианте, принято говорить об одном решении.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается (если это не высшая математика)