Объяснение:
Найдите сумму первых 10 членов арифметической прогрессии:
1) b₁=6,4; d=0,8 b₁₀= b₁+9d=6,4+0,8*9=6,4+7,2=13,6
Сумма равна (полусумме первого и последнего члена) умноженного на колличество членов. Полусумма - это среднее арифметическое первого и последнего,оно равно среднему арифметическомиу любой пары равноудаленной от медианы ряда.
(6,4+13,6)*10/2=100 сумма равна 100.
2)
а₁=3; а₁₀= 17 (а₁+ а₁₀)*н/2= сумма 10 членов
(3+17)*10/2=100 сумма равна 100.
3)b₁=-17,d=6 , b₁₀=-17+9*6 =37
сумма 10 членов равна (b₁+ b₁₀)*н/2=(-17+37)*10/2=100
сумма 10 членов равна 100
а) 10
б) 120
Объяснение:
Пусть а - арифметическая прогрессия, учитывающая 1 шар как 1 единицу. Тогда, d = 1, так как в каждом ряду количество шаров на 1 больше, чем в предыдущем, а1 = 1, так так в первом ряду 1 шар.
а) S(n) =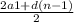 
* n = 55
Подставим а1 и d:
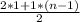* n = 55
(2 + (n - 1)) * n / 2 = 55
(2 + (n - 1)) * n = 110
(2 + n - 1) * n = 110
(n + 1) * n = 110
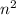+ n - 110 = 0
D = 1 - 4 * 1 * (-110) = 441 =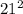 
n1 = (-1 - 21) / 2 = -11, не удовлетворяет условию
n2 = (-1 + 21) / 2 = 10
То есть, n = 10.
б) S (15) = 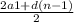* n =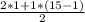 
* 15 = (2 + 14) * 15 / 2 = 120
4х^2+100x-4x^2-24x-32-x^2-29x-100=0
-x^2+47x-132=0
D=47^2+132*4=2209-528=1681=41^2 x=(-47+-41)/(-2) x=3 или x=44
Получаем две дроби 3/7 и 44/48=11/12 (т.к. знаменатель больше на 4)
2) Пусть скорость катера х. скорость по течению х+2, протв течения х-2.
Составляем уравнение
40/(х+2) + 6/(х-2)= 3
40(х-2)+6(х+2)-3(х+2)(х-2)=0
-3х^2 +46х -56=0
х1=14
х2=8/6(слишком маленькая для катера)
Значит ответ будет 14.